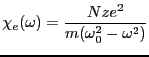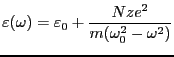: 抵抗がある場合
: 変動する電磁場と物質
: 物質中のマクスウェルの方程式
目次
誘電体中の振動電界の振る舞いを調べるために、誘電体をモデル化した原子の集
合と考える。このモデル原子は、中心の質量の大きな原子核とそれにバネでつな
がれた電子の複合体と考える。原子核の質量は大きいので、電子の運動に比べて
原子核の運動は無視できるとする。
バネ定数を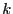 とすれば電界のない場合の運動方程式は、電子の変位を
とすれば電界のない場合の運動方程式は、電子の変位を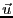 として
として
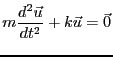 |
|
|
(3.42) |
となる。電子は固有振動数
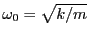 を持つことになる。
ここに、振動電界
を持つことになる。
ここに、振動電界
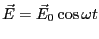 をかけると、
をかけると、
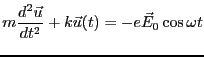 |
|
|
(3.43) |
となり、外力の加わった振動子の運動方程式と同じ形になる。交流回路で学んだ
微分方程式の解法を用いて、
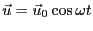 とおいて式
変形すると、
とおいて式
変形すると、
となる。従って
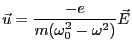 |
|
|
(3.44) |
となる。1分子に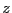 この電子があるとすれば、1分子に生じる分極
この電子があるとすれば、1分子に生じる分極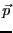 は、
は、
ただし、
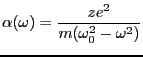 |
|
|
(3.47) |
で、これが分子の分極率である。ここで注目すべき点は振動電界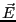 の振
動数
の振
動数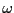 が電子の固有振動数
が電子の固有振動数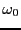 に近いところで、分極が非常に大き
くなる点である。
に近いところで、分極が非常に大き
くなる点である。
マクロな物質でも、外部から与えられる電界が分子にもそのまま作用すると考え
ると、(この近似は分極の効果が小さい時に正しい)単位体積中の分子の数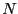 を式3.55にかけて、
を式3.55にかけて、
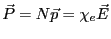 |
|
|
(3.48) |
ただし、
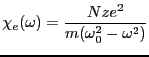 |
|
|
(3.49) |
となる。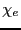 は電気感受率である。そして、誘電率も周波数依存性を持ち、
は電気感受率である。そして、誘電率も周波数依存性を持ち、
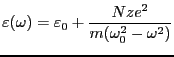 |
|
|
(3.50) |
となる。周波数
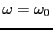 で関数は発散するが、これは電子の運動に
おける抵抗の効果を考慮していないからである。
で関数は発散するが、これは電子の運動に
おける抵抗の効果を考慮していないからである。
図 3.17:
誘電率の周波数依存性(抵抗のない場合)
|
|




: 抵抗がある場合
: 変動する電磁場と物質
: 物質中のマクスウェルの方程式
目次
Administrator
平成25年7月6日
![]() とすれば電界のない場合の運動方程式は、電子の変位を
とすれば電界のない場合の運動方程式は、電子の変位を![]() として
として
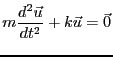
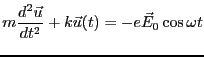
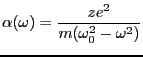
![]() を式3.55にかけて、
を式3.55にかけて、