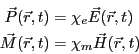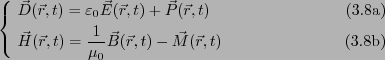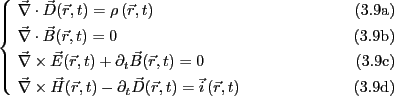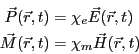物質中のマクスウェルの方程式

真空中と異なり、物質中では磁化電流や分極電荷の移動に関わる「電流」を考慮しないといけない。静磁場の基本法則について考察した場合と同様に、分極や磁化を取り入れた電束密度と磁界を次のように導入する。
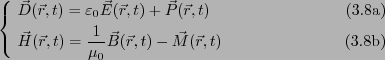
$\begin{subnumcases} {} \vec{D}(\vec{r},t) = \varepsilon_0 \vec{E}(\vec{r},t) +... ...},t) = \frac{1}{\mu_0} \vec{B}(\vec{r},t)- \vec{M}(\vec{r},t) \end{subnumcases}$
そして、以下のマクスウェルの方程式が物質中で成立するとして、議論を進める。
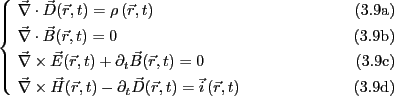
$\begin{subnumcases} {} \vec{\nabla}\cdot \vec{D}(\vec{r},t) = \rho (\vec{r},t)... ...c{r},t) -\partial_t \vec{D}(\vec{r},t) = \vec{i} (\vec{r},t) \end{subnumcases}$
時間変動する電磁場を考える場合、静的な電磁場と違って物質の時間応答の遅れを考慮する必要がある。そのために以下の式が成り立たないこともある。

$\begin{eqnarray*} \vec{P}(\vec{r},t) &=& \chi_e \vec{E}(\vec{r},t) \\ \vec{M}(\vec{r},t) &=& \chi_m \vec{H}(\vec{r},t) \end{eqnarray*}$

Administrator 平成25年7月6日