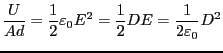: 問題2.4.14
: 導体
: 問題2.4.13
目次
静電場のエネルギー
キャパシターに電荷を蓄える場合に必要な仕事を考察する。
キャパシターの電位が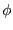 の時には電荷
の時には電荷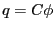 が蓄えられている。
ここに微少電荷
が蓄えられている。
ここに微少電荷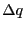 を無限遠点から運んで、電荷を
を無限遠点から運んで、電荷を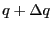 にするために必要な仕事は
にするために必要な仕事は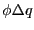 である。よって、
電荷
である。よって、
電荷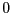 から
から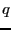 まで蓄えるのに必要な仕事
まで蓄えるのに必要な仕事 は
は
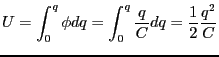 |
|
|
(2.52) |
となる。
図 2.10:
![\includegraphics[bb=10 520 600 830,width=8cm]{fig6b.eps}](img732.png) |
平行平板コンデンサーを考えれば、
となる。ここで、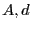 はそれぞれ極板面積、極板間隔であり、
はそれぞれ極板面積、極板間隔であり、
 は極板間の体積である。
は極板間の体積である。
この仕事は電場のエネルギーとして極板間の空間に蓄えられていると
考えることもできる。この電場のエネルギーの密度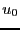 は
は
である。
Administrator
平成25年7月6日
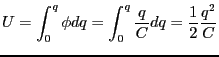
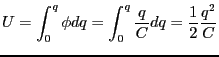
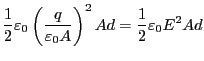
![]() は
は