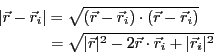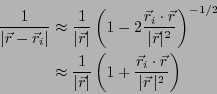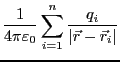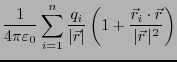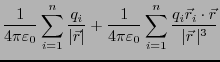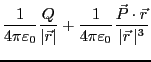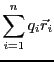: 問題2.2.19
: 電場の性質
: 問題2.2.18
目次
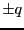 の点電荷の対の間隔
の点電荷の対の間隔
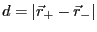 を
を
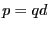 を一定に保ちながら、
小さくした極限を考える。そのような対象を電気双極子と呼び、
ベクトル
を一定に保ちながら、
小さくした極限を考える。そのような対象を電気双極子と呼び、
ベクトル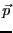 を用いて表す。
を用いて表す。
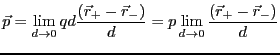 |
|
|
(2.31) |
電気双極子によって、作られる電位は
となる。
密集した多数の点電荷による十分遠方の電位を近似的に求める方法について
考えよう。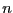 個の点電荷
個の点電荷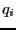 が位置
が位置
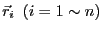 に存在
する。ただし、
に存在
する。ただし、
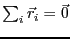 となるように原点を決める。
位置
となるように原点を決める。
位置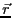 における電位は
における電位は
であるから、
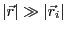 の条件を適用すると
の条件を適用すると
と近似できる。電位を求める式に代入すると、
となる。ここで、
である。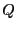 は全電荷、
は全電荷、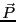 は電荷のモーメントである。
は電荷のモーメントである。




: 問題2.2.19
: 電場の性質
: 問題2.2.18
目次
Administrator
平成25年7月6日
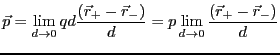
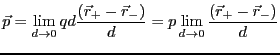
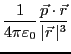
![]() 個の点電荷
個の点電荷![]() が位置
が位置
![]() に存在
する。ただし、
に存在
する。ただし、
![]() となるように原点を決める。
位置
となるように原点を決める。
位置![]() における電位は
における電位は