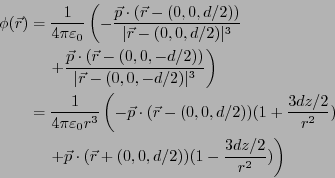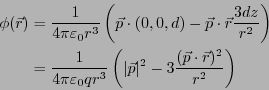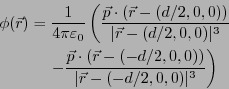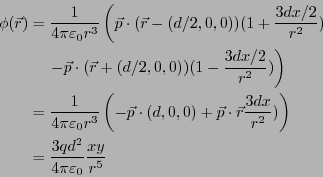: 電束
: 電気双極子
: 電気双極子
目次
以下の場合について、電荷から十分遠方における電位を求めよ。
- 3個の点電荷
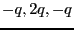 が間隔
が間隔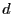 で直線上に並んでいる場合。
で直線上に並んでいる場合。
- 4個の点電荷
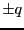 が1辺
が1辺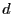 の正方形の角頂点に置かれている場合。隣り
合う電荷の符号は異なっているものとする。
の正方形の角頂点に置かれている場合。隣り
合う電荷の符号は異なっているものとする。
===== 解答 =====
- 2個の電気双極子
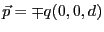 がそれぞれ
がそれぞれ
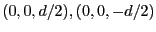 に置かれている場合を考えれ
ば良い。
に置かれている場合を考えれ
ば良い。
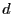 について1次までとると、
について1次までとると、
- 2個の双極子
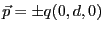 がそれぞれ
がそれぞれ
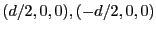 に置かれてると考えれば良い。
に置かれてると考えれば良い。
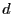 について1次までとると、
について1次までとると、
Administrator
平成25年7月6日