: 静電場の微分法則
: 電場の性質
: 問題2.2.19
目次
電束
静電場は目に見えず、直感的に理解することが難しい。そこで、
水の流れとの対比を行うことによって、理解の助けとしよう。
空間中に水の流れを考えると、空間の各点毎にそこを流れる水が存在する。
言い換えると水の流れを規定するためには、各点毎に流速を表すベクトルを
決める必要がある。このように、各点毎にベクトルが与えられるような空間を
ベクトル場と呼ぶ。水の流れの場を
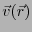 と表すこととしよう。
ある閉曲面
と表すこととしよう。
ある閉曲面 を考えて、そこでの流速の面積分
を考えて、そこでの流速の面積分
を考えよう。この面積分はこの閉曲面の中に水のわき出し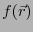 の総量に
等しいはずである。式で表すと、
の総量に
等しいはずである。式で表すと、
となる。ここで、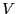 は閉曲面
は閉曲面 で囲まれる体積である。
で囲まれる体積である。
真空中の電場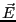 に対して
に対して
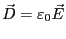 |
|
|
(2.36) |
となるベクトルを定義し、「電束密度」と呼ぶ。
ガウスの法則は以下のようになる。
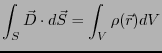 |
|
|
(2.37) |
となる。
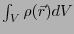 は面
は面 に囲まれた体積
に囲まれた体積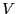 の中に存在する
全電荷量になっている。水の流れと比較すると、
の中に存在する
全電荷量になっている。水の流れと比較すると、
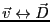 、
、
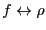 となっている
ことがわかるであろう。
となっている
ことがわかるであろう。
静電場の場合、電荷が存在しなければ
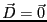 である。水の流れ場の
場合はわき出しが存在しなくても、
である。水の流れ場の
場合はわき出しが存在しなくても、
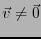 となる場合がある。
それは渦が存在する場合である。渦がある条件は
となる場合がある。
それは渦が存在する場合である。渦がある条件は
と表すことができる。ここで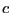 はある閉曲線であり、上の式は閉曲線
はある閉曲線であり、上の式は閉曲線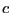 に
沿っての線積分である。
従って、静電場と水の流れ場との対比を完全に
するためには、静電場では渦がないという条件
に
沿っての線積分である。
従って、静電場と水の流れ場との対比を完全に
するためには、静電場では渦がないという条件
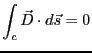 |
|
|
(2.38) |
が必要となる。
Administrator
平成25年7月6日
![]() に対して
に対して
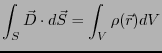
![]() である。水の流れ場の
場合はわき出しが存在しなくても、
である。水の流れ場の
場合はわき出しが存在しなくても、
![]() となる場合がある。
それは渦が存在する場合である。渦がある条件は
となる場合がある。
それは渦が存在する場合である。渦がある条件は