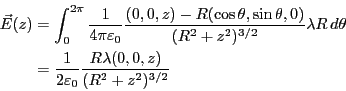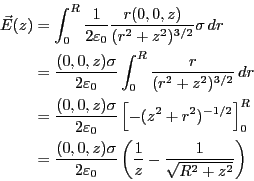: 電気力線
: 電荷のつくる電場
: 問題2.2.3
目次
以下の場合の電場を求めよ。
- 半径
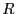 の円周上に電荷が一様に電荷密度
の円周上に電荷が一様に電荷密度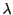 で分布している場合に、
円周の中心を通って円周が作る面に垂直な直線上の電場。
で分布している場合に、
円周の中心を通って円周が作る面に垂直な直線上の電場。
- 半径
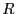 の円板上に電荷が一様に電荷密度
の円板上に電荷が一様に電荷密度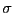 で分布している場合に、
円板の中心を通って円板が作る面に垂直な直線上の電場。
で分布している場合に、
円板の中心を通って円板が作る面に垂直な直線上の電場。
- 無限に広い平面上に電荷が一様に電荷密度
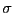 で分布している場合に、
空間の任意の点での電場。
で分布している場合に、
空間の任意の点での電場。
===== 解答 =====
円周はxy面内にあるとし、考えている直線をz軸とする。
- 円周上の
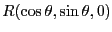 における微少線要素
における微少線要素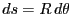 が作
る電場は、
が作
る電場は、
- 円盤を半径
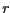 で幅
で幅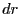 の細い輪に分割すると、それぞれの輪に対しては上の解を用
いることができる。このとき、電荷の線密度は
の細い輪に分割すると、それぞれの輪に対しては上の解を用
いることができる。このとき、電荷の線密度は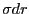 となる。
となる。
-
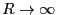 にすれば良いので、
にすれば良いので、
となる。
Administrator
平成25年7月6日