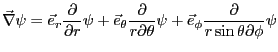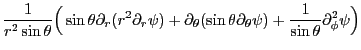: 円柱座標系
: 極座標系
: 球の体積
目次
ラプラス方程式とは、
あるいは、
と表される方程式である。Maxwellの方程式の1番目の式(電荷の保存則)が
この形になっているので、電磁気学では非常に重要な方程式である。
 は、
は、
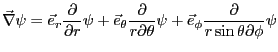 |
|
|
(1.11) |
| |
|
|
|
となる。これは、点
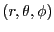 から、微小変化
から、微小変化
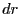 を行ったときの点の移動距離は
を行ったときの点の移動距離は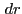 、微小変化
、微小変化
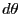 を行ったときの点の移動距離は
を行ったときの点の移動距離は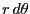 、微小変化
、微小変化
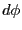 を行ったときの点の移動距離は
を行ったときの点の移動距離は
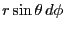 であることから、推測できるだろう。証明は文献[4]を
参照のこと。
であることから、推測できるだろう。証明は文献[4]を
参照のこと。
また、
である。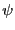 が
が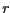 だけの関数である場合は、ラプラス方程式は
だけの関数である場合は、ラプラス方程式は
と非常に簡単になる。




: 円柱座標系
: 極座標系
: 球の体積
目次
Administrator
平成25年7月6日
![]() は、
は、