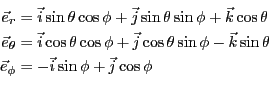: 球の体積
: 直交座標系とその応用
: デカルト座標系
目次
点対称な問題、例えば
原点に点電荷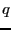 があり、その周囲の電界の様子を求める。
があり、その周囲の電界の様子を求める。
ような場合、次のような極座標系をとれば便利である。
空間上のある点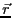 を考える。これらの変数が
他の変数
を考える。これらの変数が
他の変数
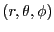 によって、以下のように表されると
する。
によって、以下のように表されると
する。
この
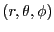 を極座標と言う。直感的には、
を極座標と言う。直感的には、
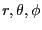 は
それぞれ、原点からの距離、緯度、経度を表す変数である。
は
それぞれ、原点からの距離、緯度、経度を表す変数である。
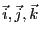 と同様なベクトルを定義しておくと、
便利である。極座標の場合は、
以下のように各点毎に異なった直交した3つのベクトルを定義しなければならない。
と同様なベクトルを定義しておくと、
便利である。極座標の場合は、
以下のように各点毎に異なった直交した3つのベクトルを定義しなければならない。
各点毎に3つの直交したベクトルを考えなければならないので、
極座標は一見とっつきにくいかも分からない。しかしながら、極座標を
用いることによって、問題が非常に簡単になる場合がある。
Administrator
平成25年7月6日
があり、その周囲の電界の様子を求める。
![]() を考える。これらの変数が
他の変数
を考える。これらの変数が
他の変数
![]() によって、以下のように表されると
する。
によって、以下のように表されると
する。
![]() と同様なベクトルを定義しておくと、
便利である。極座標の場合は、
以下のように各点毎に異なった直交した3つのベクトルを定義しなければならない。
と同様なベクトルを定義しておくと、
便利である。極座標の場合は、
以下のように各点毎に異なった直交した3つのベクトルを定義しなければならない。