準定常電流

3.1.5において定常電流の考えを導入した時、変位電流に対する考察は 全くされていなかった。ここで、準定常電流の準定常の意味を考えて見よ う。

交流回路における通常の電流と変位電流の大きさを比較してみよう。導体内部で の電界が

$$\begin{eqnarray*} \vec{E}(\vec{r},t) = \vec{E}_0 \sin \omega t \end{eqnarray*}$$

と時間変化すると仮定する。通常の電流の密度は電気伝導度を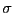$\sigma$として、

$$\begin{eqnarray*} \vec{i}(\vec{r},t) = \sigma \vec{E}_0 \sin \omega t \end{eqnarray*}$$

となる。一方、変位電流の密度は、

$$\begin{eqnarray*} \vec{i}_d(\vec{r},t) = \varepsilon_0 \frac{\partial \vec{E}}{\partial t} = \varepsilon_0 \omega \vec{E}_0 \cos \omega t \end{eqnarray*}$$

となる。変位電流が通常の電流に対して無視できる条件は、

$$\begin{eqnarray*} \omega \ll \frac{\sigma}{\varepsilon_0 }\sim 10^{18} \mathrm{s^{-1}} \end{eqnarray*}$$

となる。従って、周波数がよほど高くない限り、準定常電流を仮定し変位電流 を無視しても問題ない。