Research

1. Nonperturbative quantum analysis via resurgence theory

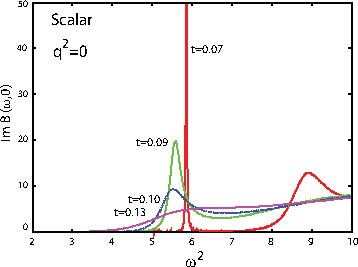
In quantum theories, we often use perturbative calculation based on series-expansion of physical quantities. In particular, it plays an essential role in the study of particle physics and quantum field theory. However, the perturbative series is divergent and one cannot analyze non-perturbative physics in the region of large coupling constant. Recently, based on the mathematical notions as Borel resummation and Stokes phenomena, it has been pointed out that the divergence of the perturbative series can include the information of non-perturbative physics (resurgent structure). In our lab., we investigate the resurgent structure in quantum mechanics and quantum field theories.

H.Nishimura, T.Fujimori, T.Misumi, M.Nitta, N.Sakai, JHEP06(2022)151
T.Fujimori, M.Honda, S.Kamata, T.Misumi, N.Sakai, T.Yoda PTEP02(2021)103B04
N.Sueishi, S.Kamata, T.Misumi, M.Unsal, JHEP12(2020)114
T.Fujimori, S.Kamata, T.Misumi, M.Nitta, N.Sakai, JHEP02(2019)190
T.Fujimori, M.Honda, S.Kamata, T.Misumi, N.Sakai, PTEP(2018)123B03
T.Fujimori, S.Kamata, T.Misumi, M.Nitta, N.Sakai, PRD94,105002(2016)
T.Misumi, M.Nitta, N.Sakai, JHEP09(2015)157
T.Misumi, M.Nitta, N.Sakai, JHEP06(2014)164

Left:Borel singularity. Center:Stokes phenomenon. Right:Bion configuration.

2. Phase diagram and confinement in compactified gauge theory

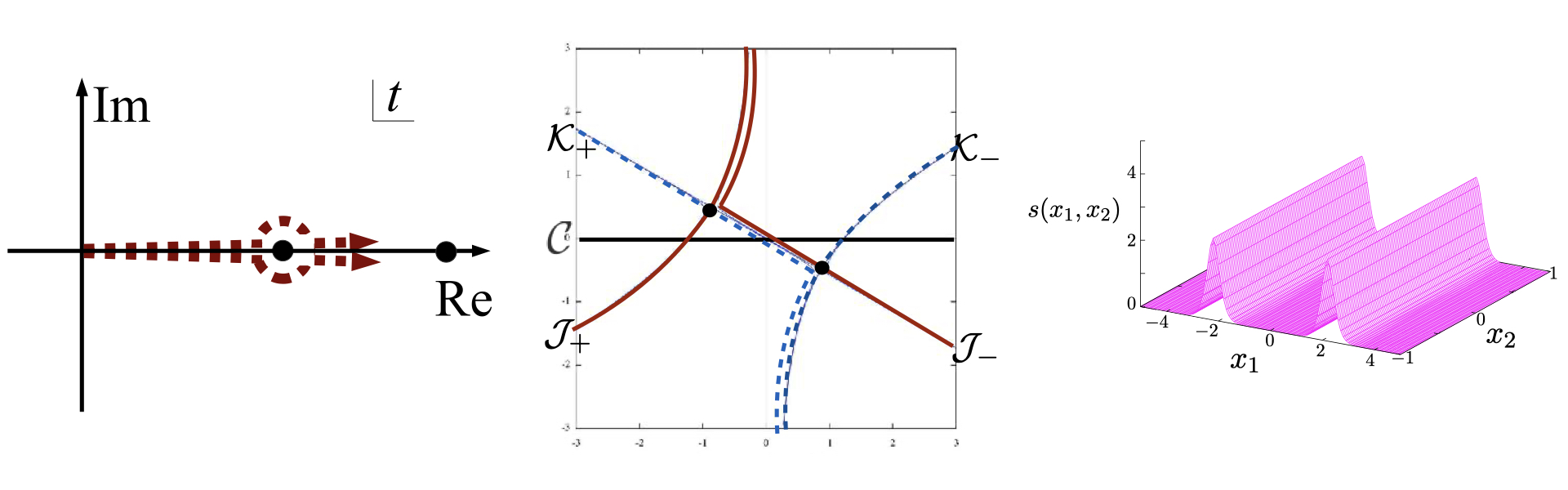
The gauge theories on compactified spacetime manifolds involve interesting phenomena including spontaneous breaking of gauge symmetry, which can be analyzed easily for small compactification radius. In our lab., we investigate phase structure for confinement and symmetries for such theories and study how the confining phase is connected to the realistic gauge theory by use of lattice simulations. We also use 't Hooft anomaly matching to make restrictions on the phase structure of QCD and 2d sigma models.

T.Fujimori, E.Itou, T.Misumi, M.Nitta, N.Sakai, JHEP08(2020)011
T.Misumi, Y.Tanizaki, M.Unsal, JHEP07(2019)018
M.Hongo, T.Misumi, Y.Tanizaki, JHEP02(2019)070
Y.Tanizaki, T.Misumi, N.Sakai, JHEP12(2017)056
T.Iritani, E.Itou, T.Misumi, JHEP11(2015)159
T.Misumi, T.Kanazawa, JHEP06(2014)181

Left:Phase diagram of QCD(adj.) on R3 x S1. Center:Polyakov-loop VEV of Z3-QCD. Right:Polyakov-loop distribution of CP2 model.

3. Lattice formulations and its applications

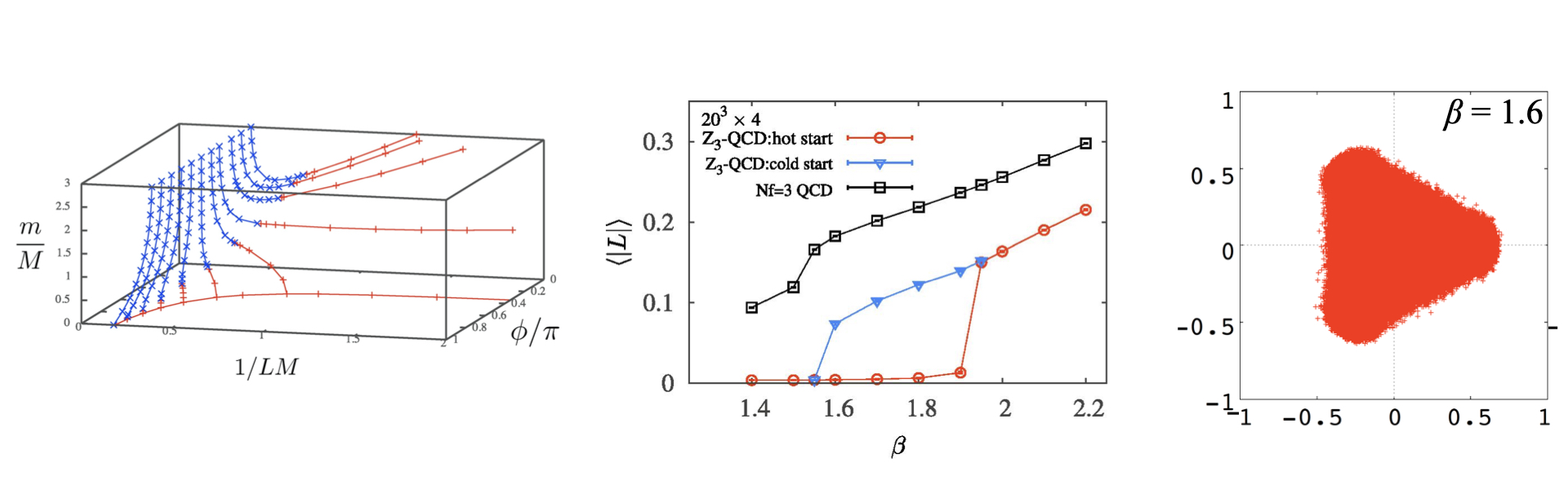
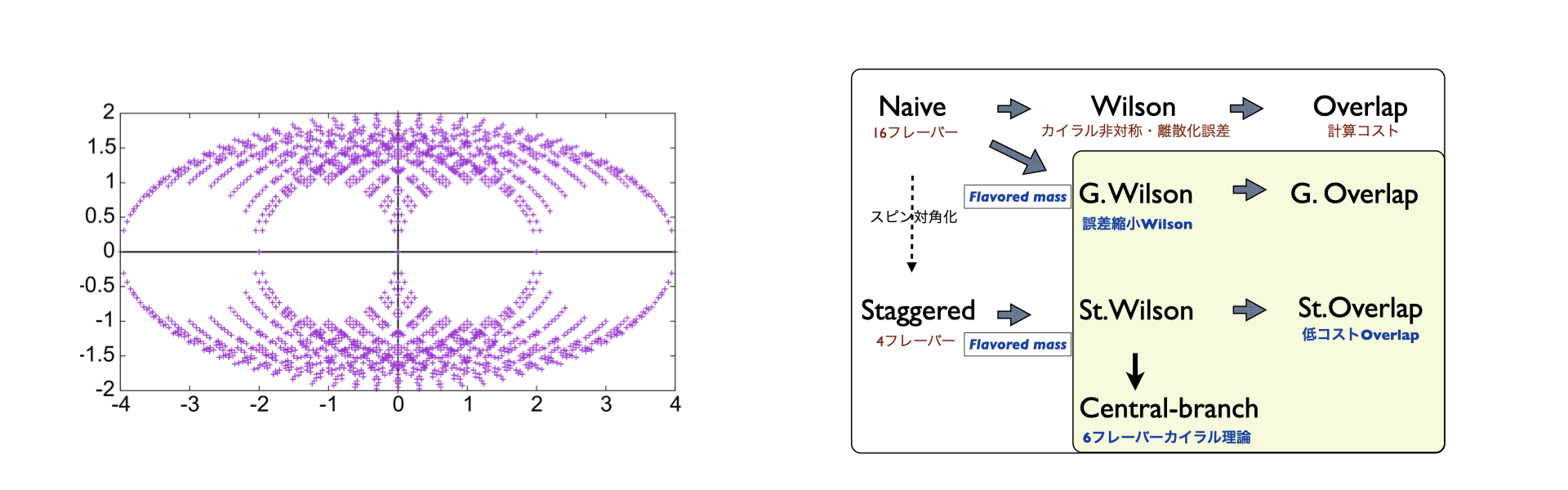
Lattice gauge theory is one of the non-perturbative formulations of quantum field theories, where field variables are defined on the lattice sites or links. Monte-Carlo calculation of path integral of this theories has been performed and has given physical results successfully. As a result of discretization of spacetime manifold, there emerge several serious problems especially in quark sectors. In our lab. we propose novel formulations to resolve these problems and study their applications to numerical simulations.

J.Yumoto, T.Misumi, JHEP02(2022)104
T.Misumi, J.Yumoto, PRD102,034516(2020)
T.Misumi, JHEP12(2013)063
T.Misumi, JHEP08(2012)068
T.Misumi, T.Z.Nakano, T.Kimura, A.Ohnishi, PRD86,034501(2012)
M.Creutz, T.Kimura, T.Misumi, PRD83,094506(2011)
M.Creutz, T.Misumi, PRD82,074502(2010)

Left:Dirac eigenvalues of Central-branch fermion. Right:Relations of lattice fermions

4. Supersymmetric gauge theories on discretized spacetime

In the extended supersymmetric(SUSY) gauge theories, some of physical quantities can be derived exactly. We successfully define 2d N=2 SUSY Yang-Mills theory on discretized 2-manifold and obtain physical quantities analytically and numerically to study its non-perturbative properties.

S.Kamata, S.Matsuura, T.Misumi, K.Ohta, PTEP(2016)123B01
S.Matsuura, T.Misumi, K.Ohta, PTEP(2015)033B07
S.Matsuura, T.Misumi, K.Ohta, PTEP(2014)123B01

Field variables of SUSY Yang-Mills theory on discretized spacetime

5. Condensed-matter physics from field-theoretical viewpoints

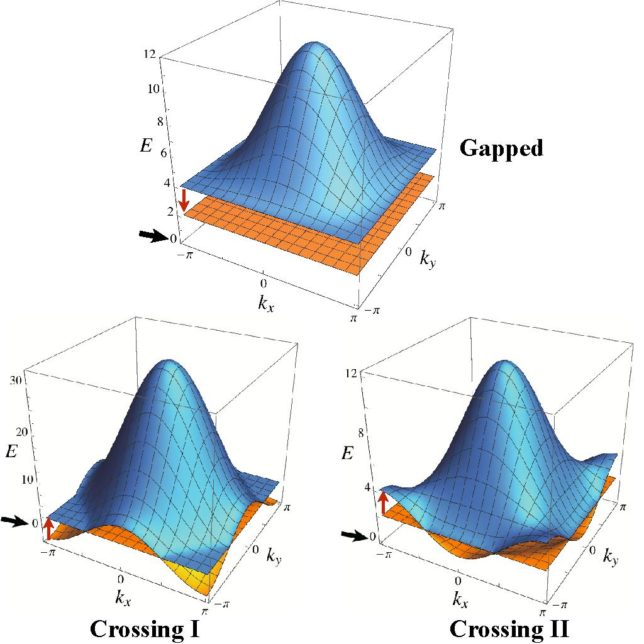
Condensed-matter systems such as graphene and topological insulators have been studied and understood well by use of quantum field theories. We focus on graphenes and flat-band models and investigate extension of the models, topological properties and electromagnetic response.

T.Misumi, H.Aoki, PRB96,155137(2017)
T.Kimura, T.Misumi, PTP123,63(2010)
T.Misumi, K.Shizuya, PRB77,195423(2008)

6. Holographic QCD models

Gauge/gravity correspondence is one of tools to study non-perturbative aspects of quantum field theories. Superstring theory implies the equivalence of a certain quantum gauge theory and a certain classical gravitational theory in a large-N limit. The gravitational model corresponding to QCD is called holographic QCD model. We study finite-temperature QCD systems by use of such holographic QCD models.

M.Fujita, K.Fukushima, T.Kikuchi, T.Misumi, M.Murata, PRD81,065024(2010)
M.Fujita, K.Fukushima, T.Misumi, M.Murata, PRD80,035001(2009)