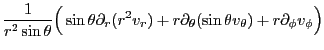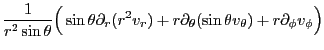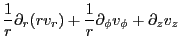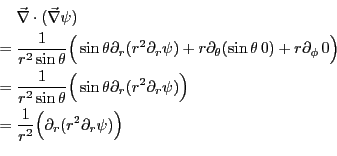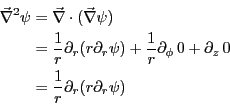: 近似計算
: 円柱座標系
: 問題1.5.3
目次
極座標と円柱座標の場合に
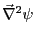 を計算せよ。
ただし、極座標の場合は
を計算せよ。
ただし、極座標の場合は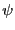 が
が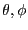 に依存せず、
円柱座標の場合には
に依存せず、
円柱座標の場合には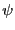 が
が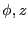 に依存しない場合を考えよ。
に依存しない場合を考えよ。
ヒント
極座標の場合、
である。また、
円柱座標の場合、
である。
===== 解答 =====
-
を計算する。ここで、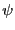 は動径方向のみの依存性を持つので、
は動径方向のみの依存性を持つので、
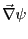 は動径方向の成分しかもたない。すなわち、
は動径方向の成分しかもたない。すなわち、
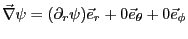 と表すことができる。従って、ヒントの式を使って、
と表すことができる。従って、ヒントの式を使って、
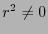 であるから,ラプラス方程式は
であるから,ラプラス方程式は
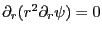 と表される.
と表される.
- 同様に、与えられた条件から
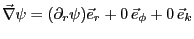 となるはずである。従って、ヒントの式を使って、
となるはずである。従って、ヒントの式を使って、
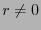 であるから,ラプラス方程式は
であるから,ラプラス方程式は
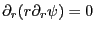 と表される.
と表される.
Administrator
平成25年7月6日