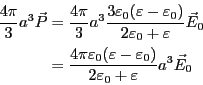: 磁性体
: 静電界の境界条件
: 問題3.4.8
目次
誘電率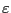 の誘電体球(半径
の誘電体球(半径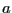 )を一様な電界
)を一様な電界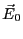 の中においた。
球に生じる電気双極子の大きさを求めよ。
の中においた。
球に生じる電気双極子の大きさを求めよ。
===== 解答 =====
誘電分極により、球の内部には反電場
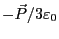 が生じる。したがっ
て、誘電体球内部の電界は、
が生じる。したがっ
て、誘電体球内部の電界は、
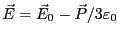 とな
る。一方、定義より、
とな
る。一方、定義より、
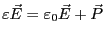 であるか
ら、
であるか
ら、
となる。
よって、球全体の双極子モーメントは、
となる。
Administrator
平成25年7月6日
![]() が生じる。したがっ
て、誘電体球内部の電界は、
が生じる。したがっ
て、誘電体球内部の電界は、
![]() とな
る。一方、定義より、
とな
る。一方、定義より、
![]() であるか
ら、
であるか
ら、