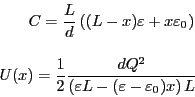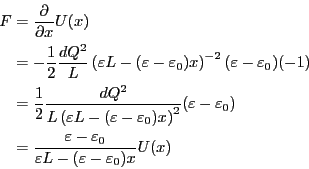: 問題3.4.9
: 静電界の境界条件
: 問題3.4.7
目次
平行平板キャパシターに誘電率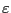 の誘電体をいれた。このキャパシター
に蓄えられている電荷
の誘電体をいれた。このキャパシター
に蓄えられている電荷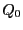 は一定である。
は一定である。
- 誘電体がある場合
とない場合の極板間の電界の様子を示し、容量の比を求めよ。
- 極板間から誘電体を引き出すために必要な力はいくらか?極板は1辺
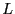 の
正方形で辺に平行に誘電体を動かす。なお誘電体も1辺
の
正方形で辺に平行に誘電体を動かす。なお誘電体も1辺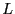 の正方形で、
その厚さは極板間の距離
の正方形で、
その厚さは極板間の距離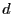 に等しい。
に等しい。
===== 解答 =====
- 図は省略。ただし、分極電荷のために、誘電体中(電極間)の電界は弱くなる
ことを図示すれば良い。
容量比は
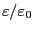 で大きくなる。
で大きくなる。
- 誘電体の位置を
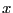 とすると、
とすると、
である。力は、
となる。
Administrator
平成25年7月6日
![]() で大きくなる。
で大きくなる。