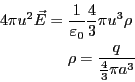: 問題3.4.3
: 静電界の境界条件
: 問題3.4.1
目次
分極の生じる第2の機構について考察する。原子を正電荷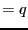 の点電荷と、それ
を中心とする半径
の点電荷と、それ
を中心とする半径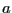 の球内に一様な負電荷(合計は
の球内に一様な負電荷(合計は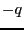 )からなると考えよう。
ただし、負電荷の分布は変化しないと考える。
)からなると考えよう。
ただし、負電荷の分布は変化しないと考える。
- 正の点電荷が負電荷の中心から長さ
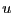 だけずれたとき、正の点電荷にはどの
ような力が働くか?
だけずれたとき、正の点電荷にはどの
ような力が働くか?
- この「原子」に一様な電界(その大きさは
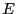 )をかけた。正電荷の位置
と負電荷の中心の位置のズレはいくらになるか?正電荷と負電荷に作用
する力のバランスを考慮して求めよ。
)をかけた。正電荷の位置
と負電荷の中心の位置のズレはいくらになるか?正電荷と負電荷に作用
する力のバランスを考慮して求めよ。
- 分極率を求めよ。
===== 解答 =====
- 分布した負電荷のつくる電界は、ガウスの定理より、
より、
となる。したがって、正の点電荷に作用する力は、
となる。
- 力のバランスを考えると、
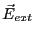 を
を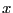 軸の正の向きにとると、
軸の正の向きにとると、
したがって、
となる。
- 仮想的な1原子の分極は
である.したがって,
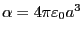 となる。
となる。
Administrator
平成25年7月6日