



: 物質中の電界と磁場
: 電気双極子の振動による電磁波
: 問題3.3.6
目次
次の式を満たすベクトルポテンシャル
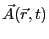 を導入しよう。
を導入しよう。
このとき、電荷も電流もない真空中のMaxwell方程式は
のように還元されることを示せ。
===== 解答 =====
真空中のMaxwellの方程式は、
であった。それぞれ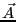 を用いて検討しよう。
を用いて検討しよう。
第1式の左辺は、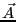 を用いて書くと
を用いて書くと
となる。すなわち、第1式は
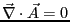 ならば、成立する。
ならば、成立する。
第2式の左辺は、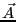 を用いて書くと
を用いて書くと
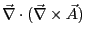 となる。この式はベクトル演算の公式より、恒等的にゼロになる。
言い替えると、
となる。この式はベクトル演算の公式より、恒等的にゼロになる。
言い替えると、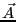 を導入すると第2式は必要なくなる。
を導入すると第2式は必要なくなる。
第3式は、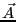 を用いて書くと
を用いて書くと
となる。この式は恒等的に成立する。
言い替えると、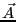 を導入すると第3式は必要なくなる。
を導入すると第3式は必要なくなる。
第4式は、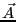 を用いて書くと
を用いて書くと
となる。左辺は公式より変形できて、
となる。ここで、
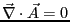 から、最終的に、
から、最終的に、
と等価になる。
Administrator
平成25年7月6日
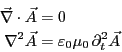
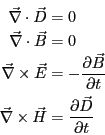
![]() を用いて書くと
を用いて書くと
![]() を用いて書くと
を用いて書くと
![]() となる。この式はベクトル演算の公式より、恒等的にゼロになる。
言い替えると、
となる。この式はベクトル演算の公式より、恒等的にゼロになる。
言い替えると、![]() を導入すると第2式は必要なくなる。
を導入すると第2式は必要なくなる。
![]() を用いて書くと
を用いて書くと
![]() を用いて書くと
を用いて書くと