



: 光速
: マクスウェルの方程式と電磁波
: 問題3.3.4
目次
微分形のマクスウェルの方程式の3番目の式3.26cより、
磁場が変化すると電場が発生する。この発生した電場が
さらに時間変化すると、今度は同じく4番目の式3.26dより
磁場が発生する。するとまた、電場が発生し、....と
空間中を伝わる波=「電磁波」が生じる。
電荷も電流もない真空中を伝わる波を考える。これらの条件を
数式で表すと、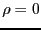 、
、
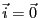 、
、
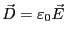 、そして
、そして
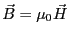 である。よって、マクスウェルの方程式は
電界
である。よって、マクスウェルの方程式は
電界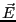 と磁場
と磁場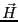 だけで表せ、
だけで表せ、
となる。ここで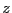 方向に伝わる平面波を考えると、すべての量は
方向に伝わる平面波を考えると、すべての量は
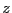 と
と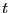 だけの関数であるから、マクスウェルの方程式は
だけの関数であるから、マクスウェルの方程式は
となる。ただし、
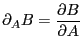 と略記
している。
と略記
している。
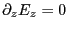 、
、
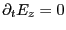 より、
より、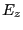 は
は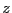 にも
にも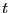 にも
よらない定数である。ここでは静電場は考慮していないので、
にも
よらない定数である。ここでは静電場は考慮していないので、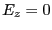 と
結論づけることができる。同様にして
と
結論づけることができる。同様にして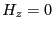 が結論できるので、電磁波は
「横波」であることがわかる。
が結論できるので、電磁波は
「横波」であることがわかる。
ここで、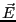 の方向を
の方向を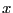 方向にとると、定義より
方向にとると、定義より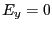 である。
この
である。
この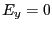 と上記の方程式を合わせて、
と上記の方程式を合わせて、
が得られる。すなわち、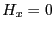 となり
となり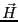 は
は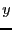 成分だけを持つ。
成分だけを持つ。
結局、マクスウェルの方程式は以下のにように簡略できる。
最初の2式は横波であることを示し、第3,4式は波に伴う電界と磁場の変動方向が
直交していることを表している。
最後の2つの方程式より、
同様に、
となるが、これらは早さが
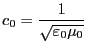 の波動方程式
である。
の波動方程式
である。
すなわち、マクスウェルの方程式より
となる波=「電磁波」の存在が予言される。この予言はマクスウェルの
よって最初になされ、ヘルツによってその存在が確認された。ただし
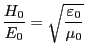 である。
である。
Administrator
平成25年7月6日
![\includegraphics[width=8cm]{fig8b.eps}](img1288.png)
![\includegraphics[width=8cm]{fig8b.eps}](img1288.png)
![]() 、
、
![]() 、
、
![]() 、そして
、そして
![]() である。よって、マクスウェルの方程式は
電界
である。よって、マクスウェルの方程式は
電界![]() と磁場
と磁場![]() だけで表せ、
だけで表せ、
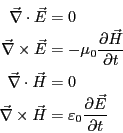

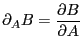 と略記
している。
と略記
している。
![]() の方向を
の方向を![]() 方向にとると、定義より
方向にとると、定義より![]() である。
この
である。
この![]() と上記の方程式を合わせて、
と上記の方程式を合わせて、
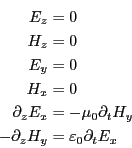
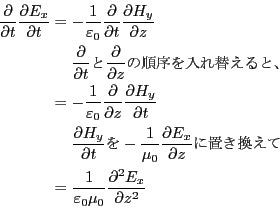
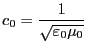 の波動方程式
である。
の波動方程式
である。
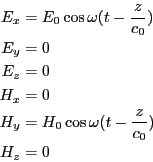
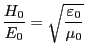 である。
である。
![\includegraphics[width=8cm]{fig8c.eps}](img1310.png)