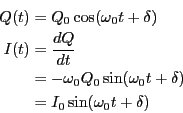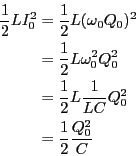: 問題3.2.6
: 電気振動
: 問題3.2.4
目次
以下の回路において抵抗がゼロの場合を考える。
- キャパシターに蓄えられる最大のエネルギーを求めよ。そのときのコイ
ルに蓄えられているエネルギーはいくらか?
- コイルに蓄えられる最大のエネルギーを求めよ。そのときの
キャパシターに蓄えられているエネルギーはいくらか?
===== 解答 =====
-
であるから、
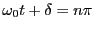 の時に、
コンデンサーに蓄えられているエネルギーは最大
の時に、
コンデンサーに蓄えられているエネルギーは最大
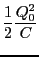 になる。このとき、
コイルの電流はゼロであるから、コイルに蓄えられている
エネルギーはゼロである。
になる。このとき、
コイルの電流はゼロであるから、コイルに蓄えられている
エネルギーはゼロである。
- 同様に考えると、
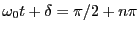 の時に、
コンデンサーの電圧はゼロになり、コイルに流れる電流は
最大になるので、そのとき
の時に、
コンデンサーの電圧はゼロになり、コイルに流れる電流は
最大になるので、そのとき
となる。
Administrator
平成25年7月6日
![\includegraphics[width=4cm]{fig86.eps}](img1143.png)