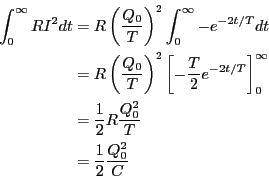: 複素インピーダンス
: 電気振動
: 問題3.2.5
目次
キャパシター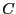 、抵抗
、抵抗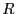 、スイッチ
、スイッチ が直列回路を構成している。
最初キャパシターには電荷
が直列回路を構成している。
最初キャパシターには電荷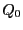 が蓄えられていた。
が蓄えられていた。
- スイッチを閉じた後のキャパシターの電圧、抵抗に流れる電流を求めよ。
- 抵抗
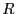 で発生するジュール熱と最初キャパシター
で発生するジュール熱と最初キャパシター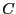 に蓄えられていた
エネルギーを比較せよ。
に蓄えられていた
エネルギーを比較せよ。
===== 解答 =====
-
だから、
となる。この微分方程式を解けば、
ただし、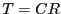 である。キャパシターに現れる電圧は
である。キャパシターに現れる電圧は
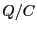 、抵抗に流れる電流は
、抵抗に流れる電流は
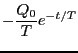 である。
である。
-
となり、最初キャパシターに蓄えられていたエネルギーに等しい。
Administrator
平成25年7月6日
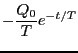 である。
である。