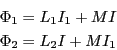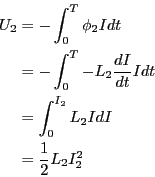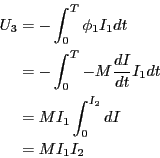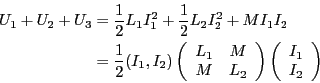: 問題3.2.5
: 電気振動
: 問題3.2.3
目次
自己インダクタンスが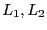 で相互インダクタンスが
で相互インダクタンスが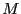 の2つの回路がある。
の2つの回路がある。
- 回路1にのみ電流
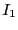 を流したときに回路に蓄えられるエネルギー
を流したときに回路に蓄えられるエネルギー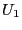 はいくらか?
はいくらか?
- コイル1の電流を一定に保ちながら、コイル2に電流を流し始める。コイ
ル2の電流が
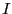 になったときに、コイル1,2を貫く磁束はいくらか?
になったときに、コイル1,2を貫く磁束はいくらか?
- 誘導起電力
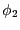 に抗してコイル2の電流を0から
に抗してコイル2の電流を0から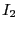 まで増加するの
に必要な仕事
まで増加するの
に必要な仕事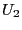 はいくらか?
はいくらか?
- コイル2の電流が0から
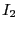 まで変化する間、誘導起電力
まで変化する間、誘導起電力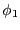 に抗し
てコイル1の電流を
に抗し
てコイル1の電流を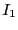 に維持するために必要な仕事
に維持するために必要な仕事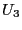 はいくらか。
はいくらか。
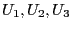 の合計を求めよ。
の合計を求めよ。
===== 解答 =====
-
-
-
だから、
-
-
Administrator
平成25年7月6日