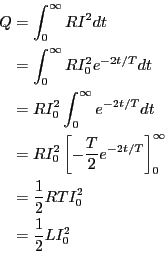: 問題3.2.3
: 電気振動
: 問題3.2.1
目次
インダクタンス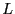 の超伝導コイルに電流
の超伝導コイルに電流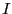 が流れていた。ところが、
わずかな残留抵抗
が流れていた。ところが、
わずかな残留抵抗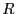 の
ために、コイルの電流は徐々に減少した。電流の時間変化を微分方程式を解くこ
とによって求めよ。
ただし、時刻
の
ために、コイルの電流は徐々に減少した。電流の時間変化を微分方程式を解くこ
とによって求めよ。
ただし、時刻 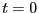 における電流を
における電流を 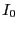 とする。
さらに、コイルの電流がゼロになる
までに、抵抗
とする。
さらに、コイルの電流がゼロになる
までに、抵抗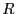 で発生するジュール熱を計算せよ。
また、それを、初めに蓄えられてい
た静磁場のエネルギーと比較せよ。
で発生するジュール熱を計算せよ。
また、それを、初めに蓄えられてい
た静磁場のエネルギーと比較せよ。
===== 解答 =====
だから、
となる。積分することによって、
となる。ただし、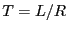 である。
である。
抵抗で発生するジュール熱は、各瞬間におけるジュール熱を積分すれば
良いので、
となる。最初コイルに蓄えられていた磁場のエネルギーと等しいことに注意する
こと。
Administrator
平成25年7月6日