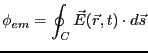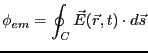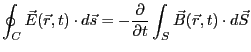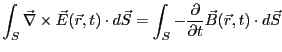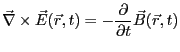電磁誘導の法則の微分形

閉回路に生じる起電力は電界の定義により、閉回路に沿った電場を積分したもの である。式で表すと、

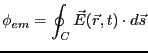$$\phi_{em} = \oint_C \vec{E}(\vec{r},t) \cdot d\vec{s}$$ (3.6)

となる。さらに電界は閉回路の有無によらず、存在することを考えると 上の式の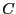$C$を単なる閉じた経路を表すものとしてもよいと考えられる。

式3.1より、

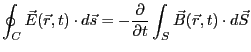$$\oint_C \vec{E}(\vec{r},t) \cdot d\vec{s} =-\frac{\partial}{\partial t}\int_S \vec{B}(\vec{r},t) \cdot d\vec{S}$$ (3.7)

となる。左辺にはストークスの定理を適用し、 右辺の積分と時間微分の順序を変えれば、

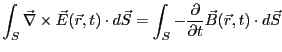$$\int_S \vec{\nabla}\times \vec{E}(\vec{r},t) \cdot d\vec{S} =\int_S -\frac{\partial}{\partial t} \vec{B}(\vec{r},t) \cdot d\vec{S}$$ (3.8)

となる。曲面$S$は任意であるから、両辺は積分の中も等しいはずである。すな わち、

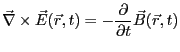$$\vec{\nabla}\times \vec{E}(\vec{r},t) = -\frac{\partial}{\partial t} \vec{B}(\vec{r},t)$$ (3.9)

でないといけない。以上により、電磁誘導の法則の微分形が得られた。