



: 電磁誘導の法則の微分形
: 電磁誘導
: 運動の相対性
目次
一様なz方向の磁場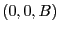 中に垂直に長方形の回路を置く。
その一辺AB(長さ
中に垂直に長方形の回路を置く。
その一辺AB(長さ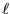 )を早さ
)を早さ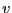 でx方向に動かす時を考える。
導線には自由電子が
存在し、それにはローレンツ力が作用する。このローレンツ力
によって自由電子はy方向に動かされ、Bの方にたまる。この荷電粒子の
分布の不均衡によってA
でx方向に動かす時を考える。
導線には自由電子が
存在し、それにはローレンツ力が作用する。このローレンツ力
によって自由電子はy方向に動かされ、Bの方にたまる。この荷電粒子の
分布の不均衡によってA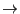 Bの向きの電界
Bの向きの電界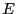 が生じる。
この電界による電子に作用する力とローレンツ力が
打ち消しあうと電子の移動はとまる。
が生じる。
この電界による電子に作用する力とローレンツ力が
打ち消しあうと電子の移動はとまる。
すなわち、
となる。
このように辺ABを動かす時に、
仮想的な電界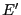 が生じその電界によって自由電子が
動いたと考えることもできる。
その仮想的な電界によるAB間の電圧は
が生じその電界によって自由電子が
動いたと考えることもできる。
その仮想的な電界によるAB間の電圧は
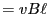 である。すなわち、
「導線を動かすことによって、起電力が生じる」と考えること
ができる。この起電力の原因はミクロに見ると自由電子に
作用するローレンツ力である。
である。すなわち、
「導線を動かすことによって、起電力が生じる」と考えること
ができる。この起電力の原因はミクロに見ると自由電子に
作用するローレンツ力である。
この場合に閉回路に生じる起電力は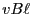 であり、
であり、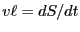 (
( は閉
回路の面積)なので、式3.1が成り立っている。
は閉
回路の面積)なので、式3.1が成り立っている。
Administrator
平成25年7月6日
![\includegraphics[width=8cm]{fig81.eps}](img1013.png)
![]() であり、
であり、![]() (
(![]() は閉
回路の面積)なので、式3.1が成り立っている。
は閉
回路の面積)なので、式3.1が成り立っている。