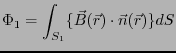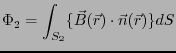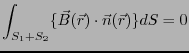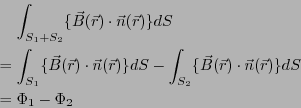: 運動の相対性
: 電磁誘導
: 電磁誘導
目次
閉回路を貫く時間的に変動する磁束を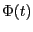 とした場合、その閉回路には
とした場合、その閉回路には
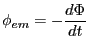 |
|
|
(3.1) |
の起電力が生じる。その閉回路を貫く磁束は磁束密度
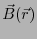 を用いて、
を用いて、
 |
|
|
(3.2) |
と表される。負号の意味は
「電磁誘導によって生じる起電力によって電流が流れた場合、その
電流の作る磁場は起電力の原因となった磁束の変化を減らす方向
に生じる」ことを意味している。このことを特に「レンツの法則」
と言うこともある。
ここで は閉回路を境界とする任意の曲面である。
は閉回路を境界とする任意の曲面である。
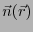 は回路の向きを決めておき、その向きに回転する右ネジの進
む向きを正とするようなその曲面に対する法線ベクトルである。
は回路の向きを決めておき、その向きに回転する右ネジの進
む向きを正とするようなその曲面に対する法線ベクトルである。
ここで、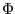 は曲面の取り方に依存しないことを証明しておこう。まず、閉回
路を境界とする任意の二つの曲面
は曲面の取り方に依存しないことを証明しておこう。まず、閉回
路を境界とする任意の二つの曲面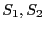 を考え、それらを貫く磁束をそれぞ
れ
を考え、それらを貫く磁束をそれぞ
れ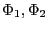 とする。
とする。
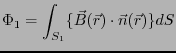 |
|
|
|
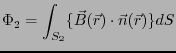 |
|
|
(3.3) |
二つの曲面をあわせたもの は閉曲面になるので、ガウスの法則により、
は閉曲面になるので、ガウスの法則により、
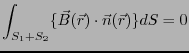 |
|
|
(3.4) |
である。ここで、曲面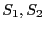 を独立に考えた場合の法線の向きと二つを組み
合わせて閉曲面を作ったときの法線の向きに注意すると、
を独立に考えた場合の法線の向きと二つを組み
合わせて閉曲面を作ったときの法線の向きに注意すると、
以上により、
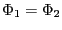 |
|
|
(3.5) |
となり、曲面 の取り方に依存しないことが証明された。
の取り方に依存しないことが証明された。
Administrator
平成25年7月6日
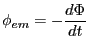

![]() は閉回路を境界とする任意の曲面である。
は閉回路を境界とする任意の曲面である。
![]() は回路の向きを決めておき、その向きに回転する右ネジの進
む向きを正とするようなその曲面に対する法線ベクトルである。
は回路の向きを決めておき、その向きに回転する右ネジの進
む向きを正とするようなその曲面に対する法線ベクトルである。
![]() は曲面の取り方に依存しないことを証明しておこう。まず、閉回
路を境界とする任意の二つの曲面
は曲面の取り方に依存しないことを証明しておこう。まず、閉回
路を境界とする任意の二つの曲面![]() を考え、それらを貫く磁束をそれぞ
れ
を考え、それらを貫く磁束をそれぞ
れ![]() とする。
とする。