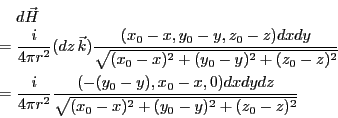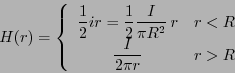: ベクトル・ポテンシャル
: アンペールの法則
: 問題2.6.13
目次
無限に長い断面が半径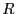 の円形の導線に電流
の円形の導線に電流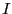 が流れている場合の磁場を
以下の手順に従って求めよ。
が流れている場合の磁場を
以下の手順に従って求めよ。
- 電流密度
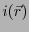 を求めよ。
を求めよ。
- ビオ-サバールの法則より磁力線には動径方向の成分がないことを説明せよ。
- アンペールの法則より磁場の大きさを求めよ。
===== 解答 =====
-
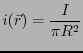 である。
である。
- 電線の中の位置
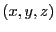 における電流の微少要素によって作られる
位置ベクトル
における電流の微少要素によって作られる
位置ベクトル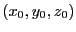 での磁場を考える。
での磁場を考える。
この式より、磁場にはz成分が存在しないことが分る。座標軸の取り方は
任意だから、点
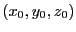 として
として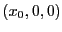 のみを考えてそこでの
磁場がy方向の成分しかないことが証明できれば十分である。その磁場は
のみを考えてそこでの
磁場がy方向の成分しかないことが証明できれば十分である。その磁場は
となる。一方、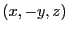 にある微少電流要素からの磁場は
にある微少電流要素からの磁場は
である。両者を足すと、磁場はy方向の成分しか存在しない。電流の分布は
y軸に対して対称だから、積分してもy方向の成分がないことが分る。
- 各点における磁場の大きさを
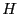 とすると、
それは導線の中心軸からの距離
とすると、
それは導線の中心軸からの距離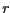 だけの関数である。
ここで、アンペールの法則を適用すると
だけの関数である。
ここで、アンペールの法則を適用すると
故に、
となる。
Administrator
平成25年7月6日
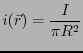 である。
である。