



: 問題2.6.7
: ビオ-サバールの法則
: ビオ-サバールの法則
目次
無限に長い(
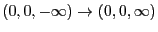 )直線電流による磁場
を考える。導線には
強さ
)直線電流による磁場
を考える。導線には
強さ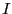 の電流が流れている。直線電流の微小部分
の電流が流れている。直線電流の微小部分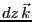 が
点
が
点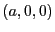 に作る微小磁場
に作る微小磁場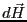 は
は
となる。ただし、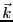 はz方向の単位ベクトルである。
これを積分することによって、磁場を求めよ。
はz方向の単位ベクトルである。
これを積分することによって、磁場を求めよ。
===== 解答 =====
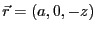 を代入すれば、
を代入すれば、
となる。これをを積分することによって、点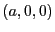 における磁場
における磁場
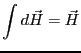 を求めることができる。
を求めることができる。
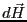 はx方向の成分を持たないこと。また、積分するとz方向の成分はキャ
ンセルすることを念頭に、y方向の大きさ
はx方向の成分を持たないこと。また、積分するとz方向の成分はキャ
ンセルすることを念頭に、y方向の大きさ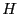 のみを計算する。
のみを計算する。
となる。ここで変数変換
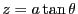 を用いた。
以上により、
を用いた。
以上により、
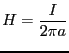 となる。
となる。
Administrator
平成25年7月6日
![]() を代入すれば、
を代入すれば、
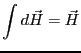 を求めることができる。
を求めることができる。
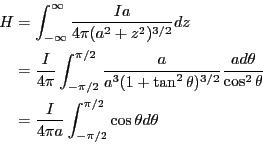
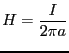 となる。
となる。