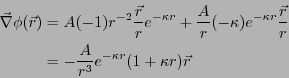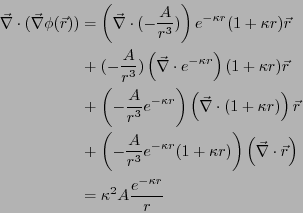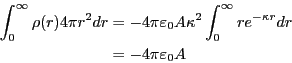: ポアソン方程式の解の性質
: ポアソン方程式
: 問題2.3.5
目次
電位
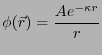 で表される。ここで、
で表される。ここで、
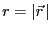 である。
である。
- 原点以外の電荷密度を求めよ。
- 原点における点電荷の大きさを求めよ。
- 原点以外に分布する全電荷を求めよ。
===== 解答 =====
- ポアソンの方程式より以下のように求めることができる。
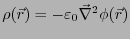 より、
より、
となる。
- 電場は
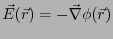 から、
から、
である。原点を中心とする微少な半径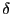 の球を考えてガウスの法則を適用
すると、
の球を考えてガウスの法則を適用
すると、
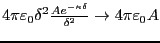 となる。
となる。
- 原点以外に分布する電荷の総和は、
となる。原点に存在する電荷と符号が逆で大きさは等しい点に注意。
Administrator
平成25年7月6日
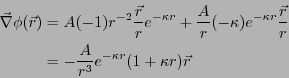
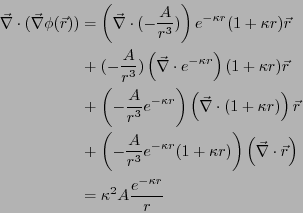
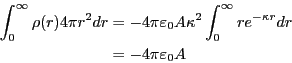
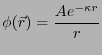 で表される。ここで、
で表される。ここで、