



: 導体
: 静電場の微分法則
: 問題2.3.6
目次
ある電荷分布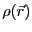 が与えられているとき、ポアソン方程式を満たす
解
が与えられているとき、ポアソン方程式を満たす
解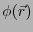 が見つかったとしよう。また、ラプラス方程式の解
が見つかったとしよう。また、ラプラス方程式の解
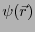 とすると、
とすると、
となり、
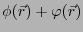 も解であることがわかる。
このように解には不定性があり、境界における条件を満たすようにして
始めて電位は決まる。
も解であることがわかる。
このように解には不定性があり、境界における条件を満たすようにして
始めて電位は決まる。
ポアソン方程式から以下の電位の性質が導かれる。
- 電位は電荷のないところで極大、極小にならない。
極大、極小では2次微分がゼロでない。すなわち、ラプラス方程式と矛盾
する。
- ある領域内に電荷が存在せず、その領域の境界での電位が一定な
らば、その領域内では電位は至る所境界における電位と等しい。
領域内で電位の空間変化があれば、領域内で極小または極小が存在するこ
とになる。しかしながら、これは領域内に電荷が存在しないという条件に
反することになる。
電荷分布と境界条件が与えられたならば、ポアソン方程式の解はただ一つに決ま
ることが以下のようにして分かる。
仮に、2つの解
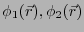 が存在すると仮定しよう。
当然、領域内で
が存在すると仮定しよう。
当然、領域内で
を満たし、境界で
を満たしている。ここで、
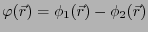 を考えると、至る所で
を考えると、至る所で
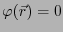 とならなければ
ならない。言い換えると、
とならなければ
ならない。言い換えると、
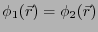 を意味しており、
解は唯一であることが分かる。
を意味しており、
解は唯一であることが分かる。
ここまで、クーロンの法則によって電荷が作る静電場の満たすべき方程式として
ガウスの法則と渦なしの法則を導いた。この2法則とポアソン方程式は等価であ
る。一方、ポアソン方程式を境界条件の下で解くことによって、静電場を完全に決
定できることを上で示した。
Administrator
平成25年7月6日
![]() が存在すると仮定しよう。
当然、領域内で
が存在すると仮定しよう。
当然、領域内で