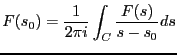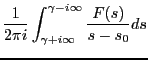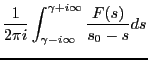: 逆ラプラス変換の例
: ラプラス変換
: インパルス応答の例
目次
ある時間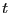 の関数
の関数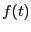 のラプラス変換
のラプラス変換
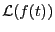 が与えられている
時、もとの関数
が与えられている
時、もとの関数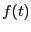 は以下の逆ラプラス変換を行うことによって求めることが
できる。
は以下の逆ラプラス変換を行うことによって求めることが
できる。
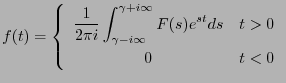 |
|
|
(9.15) |
この演算を
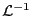 と表し、
と表し、
と書く。この公式は以下のようにして導くことができる。
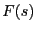 は
は
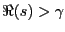 で正則であると仮定する。図9.3
のような半円を正の方向に一周する積分路
で正則であると仮定する。図9.3
のような半円を正の方向に一周する積分路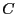 を考える。
を考える。
コーシーの積分定理より、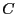 内の任意の点
内の任意の点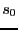 に対して
に対して
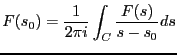 |
|
|
(9.16) |
となる。さらに、
を仮定すると円弧の部分の積分は0に収束する。従って、
である。つぎに、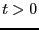 の任意の
の任意の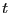 に対して
に対して
であるから、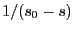 に上の積分を代入すると、
に上の積分を代入すると、
ただし、1行目から2行目は
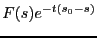 が考えている領域で
正則なので積分順序を変えることによって変形している。ラプラス変換の
定義式と式9.18を比較することにより、逆ラプラス変換の
公式が証明される。
が考えている領域で
正則なので積分順序を変えることによって変形している。ラプラス変換の
定義式と式9.18を比較することにより、逆ラプラス変換の
公式が証明される。




: 逆ラプラス変換の例
: ラプラス変換
: インパルス応答の例
目次
Administrator
平成25年1月3日
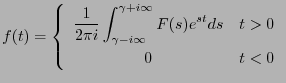
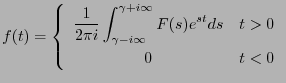
![]() は
は
![]() で正則であると仮定する。図9.3
のような半円を正の方向に一周する積分路
で正則であると仮定する。図9.3
のような半円を正の方向に一周する積分路![]() を考える。
を考える。