



: 逆ラプラス変換
: ラプラス変換
: 伝達関数
目次
コイルとコンデンサーが直列に接続された回路に対するインパルス応答を考えよ
う。系のダイナミクスを決定する微分方程式は
である。時間を無次元化するために、単位時間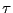 を導入する。
を導入する。
ラプラス変換を行なうと
となり、
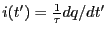 より、
より、
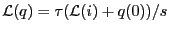 で
ある。今はインパルス応答を考えているので、
で
ある。今はインパルス応答を考えているので、
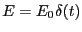 (すなわち、
(すなわち、
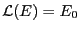 )
となる。それ以外のすべての初期条件はゼロである。よって、
)
となる。それ以外のすべての初期条件はゼロである。よって、
となる。ここで、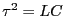 とすれば、
とすれば、
となり、線形性と表 9.1より、
となることが分かる。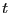 に戻すと、
に戻すと、
となる。ただし、最後の式変形には
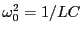 を用いた。
を用いた。
コイルとコンデンサーの直列回路にインパルスを与えると電気振動が以後継続す
るという結果が得られる。
Administrator
平成25年1月3日