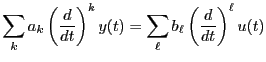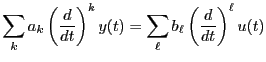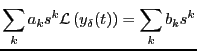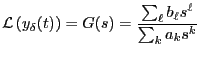: インパルス応答の例
: ラプラス変換
: 重ね合わせの原理
目次
線形時不変システムのダイナミクスが以下の微分方程式で定義されていると
しよう。
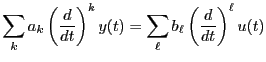 |
|
|
(9.12) |
ここで、
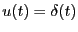 (インパルス)を考える。また、
(インパルス)を考える。また、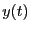 としては、
すべての初期条件がゼロの場合、すなわち
としては、
すべての初期条件がゼロの場合、すなわち
![$\frac{d^n}{dt^n}y(x)]_{t=0}=0$](img651.png) 、
考えることにする。そのような出力をここでは特別に
、
考えることにする。そのような出力をここでは特別に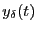 と
書くことにする。ラプラス変換を行なうと、
と
書くことにする。ラプラス変換を行なうと、
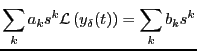 |
|
|
(9.13) |
となる。従って、デルタ関数の入力(インパルス)に対する出力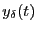 をラプラス変換すると、
をラプラス変換すると、
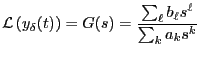 |
|
|
(9.14) |
となり、これを伝達関数と呼ぶ。微分方程式から簡単に求まることに注意。
Administrator
平成25年1月3日