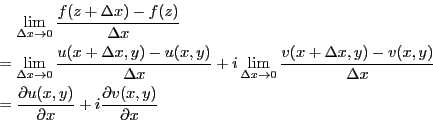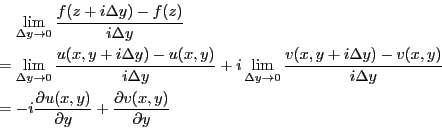: 指数関数
: 正則関数
: 複素関数の微分
目次
複素関数
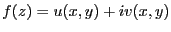 (ただし
(ただし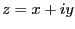 )が
)が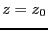 で正則である
ならば、
で正則である
ならば、
が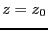 で成り立つ。これをコーシー・リーマンの関係式と言う。
で成り立つ。これをコーシー・リーマンの関係式と言う。
証明
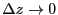 が
が
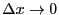 の場合を考えれば、
の場合を考えれば、
同様に
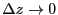 が
が
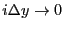 の場合を考えれば、
の場合を考えれば、
微分可能であるためには、両者は実数部分と虚数部分がそれぞれ等しくなる必要
があるので、コーシー・リーマンの関係式が得られる。
また、コーシー・リーマンの関係式を満たしていれば、微分可能になる
ことは容易に理解できるであろう。
Administrator
平成25年1月3日
![]() (ただし
(ただし![]() )が
)が![]() で正則である
ならば、
で正則である
ならば、
![]() が
が
![]() の場合を考えれば、
の場合を考えれば、