: ブロッホ方程式
: NMRの原理
: 歳差運動
目次
静磁場(磁束密度
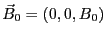 )に加え、回転磁場
を与えよう。回転する磁場の磁束密度は
)に加え、回転磁場
を与えよう。回転する磁場の磁束密度は
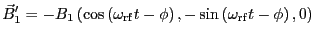 |
|
|
(11.2) |
とする。`` 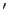 ''は回転実験室系で見ていることを表わしている。
実験室系における
''は回転実験室系で見ていることを表わしている。
実験室系における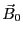 と
と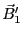 の和は早い運動をしており、
式 11.1を解くことは困難である。しかしながら、角周波数
の和は早い運動をしており、
式 11.1を解くことは困難である。しかしながら、角周波数
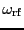 で回転する回転座標系で系を見れば、系のダイナミクスは
簡単になる。磁場は静止して見え、対応した磁束密度は
で回転する回転座標系で系を見れば、系のダイナミクスは
簡単になる。磁場は静止して見え、対応した磁束密度は
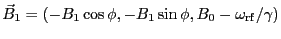 となる。
となる。
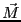 はこの実効的な磁場の回りに回転し、そのラーモア周波数は
はこの実効的な磁場の回りに回転し、そのラーモア周波数は
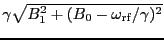 となる。
となる。
図:
回転座標系から見た回転磁場。対応した磁束密度を
表わす式は
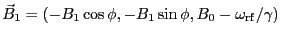 である。
である。
|
|
ラーモア周波数と同じ角速度を持つ回転磁場
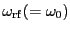 が与えられたとしよう。角速度
が与えられたとしよう。角速度
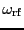 の回転座標系では
の回転座標系では
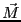 は
は
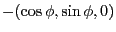 を回転の軸として
角速度
を回転の軸として
角速度
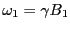 で回転する。仮に、
で回転する。仮に、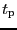 後に回転磁場が
なくなったとしよう。最初
後に回転磁場が
なくなったとしよう。最初 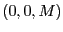 にあった
にあった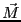 は
角度
は
角度
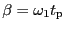 だけ傾くことになる。
だけ傾くことになる。
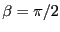 な場合、このような回転磁場は
な場合、このような回転磁場は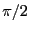 -パルス
(90
-パルス
(90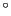 -パルス)と呼ばれ、
-パルス)と呼ばれ、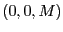 は回転座標系のx-y面内の
は回転座標系のx-y面内の
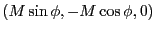 になる。従って、このようなパルスは
しばしば、
になる。従って、このようなパルスは
しばしば、
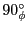 と書かれる。特に
と書かれる。特に
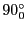 、
、
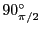 、
、
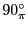 、
、
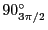 は、それぞれ
は、それぞれ
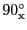 、
、
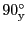 、
、
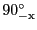 、
、
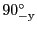 と書かれる。また、
と書かれる。また、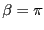 の場合は
の場合は
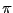 -パルス (すなわち, 180
-パルス (すなわち, 180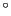 -パルス)と呼ばれ、
-パルス)と呼ばれ、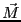 を
を
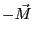 に変換する。
に変換する。
図 11.4:
高周波パルス. (a) 90
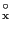 -パルスがy軸方向の
磁化に変換する。
(b) 180
-パルスがy軸方向の
磁化に変換する。
(b) 180
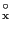 -パルスが磁化の向きを変える。
-パルスが磁化の向きを変える。
|
|
次のような振動する磁場
が回転磁場の代わりに使われることが多い。以下の恒等式が成り立つので、
振動する磁場は角速度
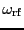 で
時計回りと反時計回りに回転する二つの磁場の重ね合わせと
考えることができる。
で
時計回りと反時計回りに回転する二つの磁場の重ね合わせと
考えることができる。
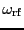 時計回りに回転する磁場は
回転座標系において静止しているように見えるが、反時計回りに
回転する磁場は
時計回りに回転する磁場は
回転座標系において静止しているように見えるが、反時計回りに
回転する磁場は
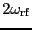 の角速度で回転しているように
見える。反時計回りに回転する磁場の効果は、通常のNMR実験の条件では
の角速度で回転しているように
見える。反時計回りに回転する磁場の効果は、通常のNMR実験の条件では
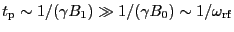 なので、平均されてなくなる。
従って、回転磁場の代わりに振動磁場を用いることができる。
なので、平均されてなくなる。
従って、回転磁場の代わりに振動磁場を用いることができる。
Administrator
平成25年1月3日
![]() が与えられたとしよう。角速度
が与えられたとしよう。角速度
![]() の回転座標系では
の回転座標系では
![]() は
は
![]() を回転の軸として
角速度
を回転の軸として
角速度
![]() で回転する。仮に、
で回転する。仮に、![]() 後に回転磁場が
なくなったとしよう。最初
後に回転磁場が
なくなったとしよう。最初 ![]() にあった
にあった![]() は
角度
は
角度
![]() だけ傾くことになる。
だけ傾くことになる。
![]() な場合、このような回転磁場は
な場合、このような回転磁場は![]() -パルス
(90
-パルス
(90![]() -パルス)と呼ばれ、
-パルス)と呼ばれ、![]() は回転座標系のx-y面内の
は回転座標系のx-y面内の
![]() になる。従って、このようなパルスは
しばしば、
になる。従って、このようなパルスは
しばしば、
![]() と書かれる。特に
と書かれる。特に
![]() 、
、
![]() 、
、
![]() 、
、
![]() は、それぞれ
は、それぞれ
![]() 、
、
![]() 、
、
![]() 、
、
![]() と書かれる。また、
と書かれる。また、![]() の場合は
の場合は
![]() -パルス (すなわち, 180
-パルス (すなわち, 180![]() -パルス)と呼ばれ、
-パルス)と呼ばれ、![]() を
を
![]() に変換する。
に変換する。