



: 電位
: 電位
: 電位
目次
質点が位置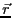 に依存した力
に依存した力
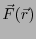 の下で、
ある基準点AからP点までゆっくりと(加速度を生じないように)移動する
場合を考える。このような移動の際、外部からその力
の下で、
ある基準点AからP点までゆっくりと(加速度を生じないように)移動する
場合を考える。このような移動の際、外部からその力
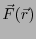 と
大きさがほとんど等しく、逆向きの力を加えないといけない。従って、
点Pまで移動する際に外から与えなければならない仕事
と
大きさがほとんど等しく、逆向きの力を加えないといけない。従って、
点Pまで移動する際に外から与えなければならない仕事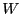 は
は
である。もしも、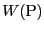 が途中の経路によらず、位置Pのみの関数である
場合に、
が途中の経路によらず、位置Pのみの関数である
場合に、
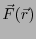 は保存力であるという。
は保存力であるという。
この保存力の下で、二つの経路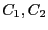 を通って基準点Aから点Pに
達する場合を考えよう。保存力の定義より、
を通って基準点Aから点Pに
達する場合を考えよう。保存力の定義より、
となる。書きかえると、
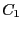 と
と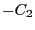 の経路は基準点Aから点Pを通って
基準点Aに戻る経路であり、閉曲線になる。その閉曲線を
の経路は基準点Aから点Pを通って
基準点Aに戻る経路であり、閉曲線になる。その閉曲線を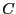 であらわすと、
であらわすと、
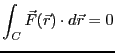 |
|
|
(2.14) |
となる。
保存力の場合、位置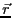 の関数
の関数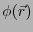 を定義して、
を定義して、
とすることができる。これは
から導かれる。




: 電位
: 電位
: 電位
目次
Administrator
平成25年7月6日
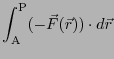
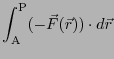
![]() を通って基準点Aから点Pに
達する場合を考えよう。保存力の定義より、
を通って基準点Aから点Pに
達する場合を考えよう。保存力の定義より、
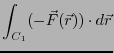
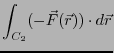
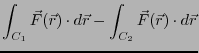
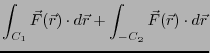
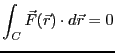
![]() の関数
の関数![]() を定義して、
を定義して、