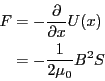: 問題3.4.13
: 静磁場の境界条件
: 問題3.4.11
目次
一様な磁化ベクトル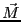 (単位体積あたり)を持つ棒磁石を2本用意する。
一つの磁石のN極ともう一方のS極を十分近づけた時、法線方向の
磁束密度は連続であるので、
隙間に生じる磁束密度
(単位体積あたり)を持つ棒磁石を2本用意する。
一つの磁石のN極ともう一方のS極を十分近づけた時、法線方向の
磁束密度は連続であるので、
隙間に生じる磁束密度
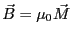 となる。
となる。
- 磁極の面積を
 として、磁極間に働く力を求めよ。
として、磁極間に働く力を求めよ。
===== 解答 =====
- 磁石の間の空間に蓄えられている磁場のエネルギー
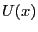 は、
は、
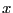 を磁石間の距離として、
を磁石間の距離として、
となる。これを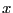 で偏微分すれば、力
で偏微分すれば、力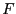 を求めることができる。
したがって、
を求めることができる。
したがって、
となる。
Administrator
平成25年7月6日