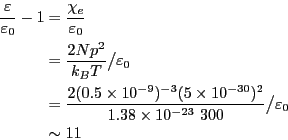: 問題3.4.5
: 静電界の境界条件
: 問題3.4.3
目次
電気感受率の概算を行おう。電気双極子モーメント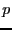 を持つ分子が電界
を持つ分子が電界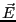 の中
に置かれた場合、電気双極子が電界の方向を向く場合と逆向きになる場合のエネ
ルギーの差は、
の中
に置かれた場合、電気双極子が電界の方向を向く場合と逆向きになる場合のエネ
ルギーの差は、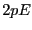 である。統計力学より、温度
である。統計力学より、温度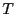 で熱振動する分子の平均の
モーメントは
で熱振動する分子の平均の
モーメントは
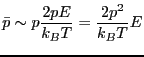 である。ここで、
である。ここで、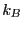 はボルツマン定数である。単位体
積中に分子が
はボルツマン定数である。単位体
積中に分子が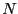 こあるとする。
ただし、誘電体の分子による電界は小さいとして、外部からかけられる電界を
分子も感じるものとして計算せよ。
こあるとする。
ただし、誘電体の分子による電界は小さいとして、外部からかけられる電界を
分子も感じるものとして計算せよ。
- 電気感受率は
となることを示せ。
- 温度が300 Kで、分子の電気双極子モーメントが
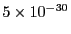 Cm
のとき、
Cm
のとき、
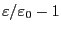 はどの程度か?分子の平均間隔は
はどの程度か?分子の平均間隔は
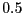 nmである。また、
nmである。また、
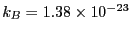 JK
JK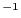 である
である
===== 解答 =====
-
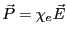 で、
で、
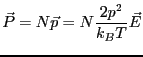 であるから、
であるから、
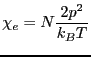 となる。
となる。
-
となる。
Administrator
平成25年7月6日
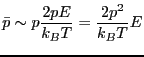 である。ここで、
である。ここで、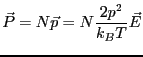 であるから、
であるから、
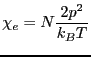 となる。
となる。