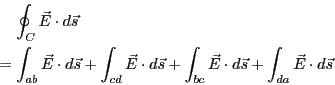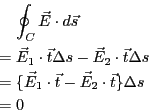: 電束密度の境界条件
: 静電界の境界条件
: 静電界の境界条件
目次
電界に関する境界条件を考えるために、図3.15のように境界上の点
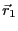 をとる。
をとる。
その周囲を囲む境界面にまたがった経路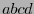 を考えて、
式3.40bの積分形
を考えて、
式3.40bの積分形
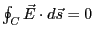 を適用する。
を適用する。
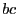 と
と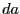 の経路はいくらでも小さくできるので、無視することにする。また、
経路
の経路はいくらでも小さくできるので、無視することにする。また、
経路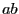 と
と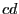 では
では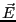 は一定と見なせるので、
は一定と見なせるので、
となる。ここで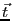 は境界面に平行な単位ベクトルである。従って、
は境界面に平行な単位ベクトルである。従って、
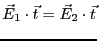 |
|
|
(3.35) |
の関係が成り立たないといけない。
Administrator
平成25年7月6日
![\includegraphics[width=7cm]{f9-6.eps}](img1364.png)
![]() を考えて、
式3.40bの積分形
を考えて、
式3.40bの積分形
![]() を適用する。
を適用する。