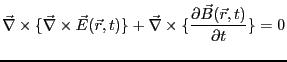: 電気双極子の振動による電磁波
: マクスウェルの方程式と電磁波
: 光速
目次
マクスウェルの方程式から波動方程式を導出するときに、まず平面波を仮定して
導出した。ここでは、ベクトル解析の手法を用いて、一般の場合の波動方程式を
導出しよう。
真空中のマクスウェルの方程式は、
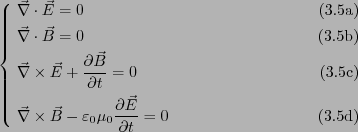
となる。まず、式3.31cの両辺に
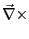 を作用させると、
を作用させると、
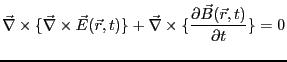 |
|
|
(3.27) |
左辺第1項はベクトル解析の公式と真空であること
(
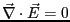 )より、
)より、
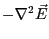 になる。
一方、式3.31dを時間で微分して空間
と時間の微分の順序を変えれば、第2項は
になる。
一方、式3.31dを時間で微分して空間
と時間の微分の順序を変えれば、第2項は
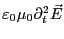 となる。以上により、
となる。以上により、
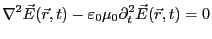 |
|
|
(3.28) |
が得られる。これは、波動方程式になっている。
Administrator
平成25年7月6日
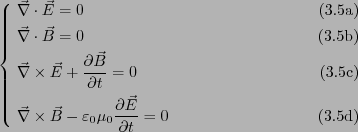
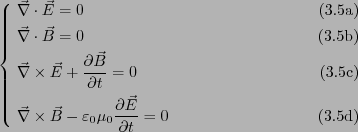
![]() を作用させると、
を作用させると、