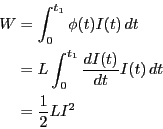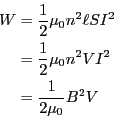: 回路
: 静磁場のエネルギー
: 静磁場のエネルギー
目次
非常に長いソレノイドの内部の磁場に蓄えられる静磁場のエネルギー
を計算することによって、式3.14を確かめて見よう。
ただし、コイルの電気抵抗は無視できるものとする。
電流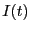 は
は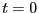 に
に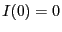 、
、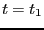 に
に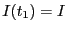 になったとする。この間電
流は増加しているので、コイルの電流増を妨げるように自己誘導起電力が生じる。
これに逆らって電流を流すためには外部から電位差
になったとする。この間電
流は増加しているので、コイルの電流増を妨げるように自己誘導起電力が生じる。
これに逆らって電流を流すためには外部から電位差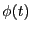
をかけないといけない。この電位差の下で電荷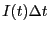 が移動するから、
電源のする仕事は
が移動するから、
電源のする仕事は
となる。時刻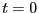 から
から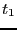 までにコイルにされた仕事は
までにコイルにされた仕事は
となる。ここで、式3.10を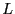 に代入すると、
に代入すると、
となる。ここで、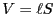 、
、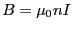 を用いた。これで、先に示した
静磁場の単位体積当たりのエネルギーが式3.14で与えられることが確か
められた。
を用いた。これで、先に示した
静磁場の単位体積当たりのエネルギーが式3.14で与えられることが確か
められた。
Administrator
平成25年7月6日
![]() は
は![]() に
に![]() 、
、![]() に
に![]() になったとする。この間電
流は増加しているので、コイルの電流増を妨げるように自己誘導起電力が生じる。
これに逆らって電流を流すためには外部から電位差
になったとする。この間電
流は増加しているので、コイルの電流増を妨げるように自己誘導起電力が生じる。
これに逆らって電流を流すためには外部から電位差![]()