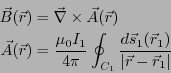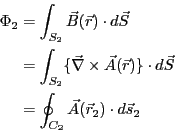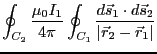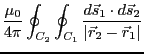: 静磁場のエネルギー
: 電磁誘導
: 問題3.1.8
目次
コイル1に電流を流してコイル2に生じる起電力から得られる相互インダクタンス
とコイル2に電流を流してコイル1に生じる起電力から得られる相互インダクタン
スは等しいことが知れらている。これを相互インダクタンスの相反定理といい、
以下のようにして証明される。
コイル1に流れる電流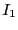 によって作られる磁束密度
はベクトルポテンシャルを用いて、
によって作られる磁束密度
はベクトルポテンシャルを用いて、
と表される。コイル2を貫く磁束は
である。最後の式変形にはストークスの定理を用いた。次に、
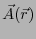 の表式を代入すると、
の表式を代入すると、
となる。従って、コイル1に電流を流した時の相互インダクタンスは
となる。コイル2に電流を流した場合の相互インダクタンス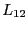 も同様に計
算できて、それは上記の式の
も同様に計
算できて、それは上記の式の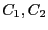 、
、
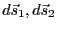 および、
および、
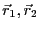 を入れ替えたも
のになる。入れ替えても結果は同じなのはあきらかである。以上により、
相互インダクタンスの相反定理は証明できた。
を入れ替えたも
のになる。入れ替えても結果は同じなのはあきらかである。以上により、
相互インダクタンスの相反定理は証明できた。
Administrator
平成25年7月6日
![]() によって作られる磁束密度
はベクトルポテンシャルを用いて、
によって作られる磁束密度
はベクトルポテンシャルを用いて、