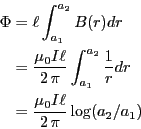: 問題3.1.6
: インダクタンス
: 問題3.1.4
目次
半径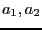 (
(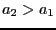 )の2本の金属管により、
同軸ケーブルを作った。一端には抵抗
)の2本の金属管により、
同軸ケーブルを作った。一端には抵抗 を、他端には電源をつなぎ電流
を、他端には電源をつなぎ電流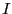 を流した。
を流した。
- アンペールの法則を用いて、同軸ケーブルの内外に生じる磁界を求めよ。
- 長さが
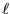 の場合、この同軸ケーブルの自己インダクタンスを求めよ。
磁束が貫く面積は
の場合、この同軸ケーブルの自己インダクタンスを求めよ。
磁束が貫く面積は
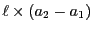 である。
である。
===== 解答 =====
- 中心導体を中心として半径
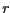 (
(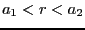 )の円を経路
として、アンペールの法則を適用する。このとき、
)の円を経路
として、アンペールの法則を適用する。このとき、
であるから、
となる。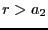 の場合には、正味の電流はないので、
の場合には、正味の電流はないので、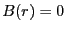 となる。
となる。
- 回路を貫く磁束は、
定義より、
となる。
Administrator
平成25年7月6日