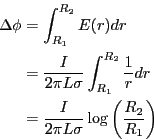: 問題2.5.4
: 導体中の電流の分布
: 導体中の電流の分布
目次
内径と外径がそれぞれ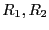 、高さが
、高さが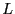 の金属製の円筒を同軸上に
配置し、その間を電気伝導度
の金属製の円筒を同軸上に
配置し、その間を電気伝導度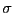 の電解質溶液で満たす。内外の円筒を
電極として電流
の電解質溶液で満たす。内外の円筒を
電極として電流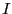 を流した場合の電気抵抗を以下の手順に従って求めよ。
を流した場合の電気抵抗を以下の手順に従って求めよ。
- 対称性から電流がどのように流れるか考察し、中心から距離
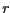 の位置で
の電流密度を求めよ。
の位置で
の電流密度を求めよ。
- オームの法則を適用して、各点における電場を求めよ。
- 電場を積分することによって、電位差を求めよ。
- 電位差と電流から抵抗を求めよ。
===== 解答 =====
- 電流は放射状に流れ、その強さは中心からの距離
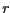 のみの関数となる。
全電流は一定だから、電流密度の大きさは
のみの関数となる。
全電流は一定だから、電流密度の大きさは
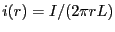 とな
る。
とな
る。
- オームの法則により、
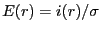 となる。
となる。
- 電位差は、
となる。
-
Administrator
平成25年7月6日