



: 問題2.5.2
: オームの法則
: オームの法則
目次
電気伝導度の異なる金属(それぞれの電気伝導度を
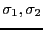 とす
る)が平面で接触し、その面に垂直に電流が
流れている。この電流の電流密度を
とす
る)が平面で接触し、その面に垂直に電流が
流れている。この電流の電流密度を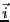 とし、境界面に現れる
電荷密度を求めよ。
とし、境界面に現れる
電荷密度を求めよ。
===== 解答 =====
接触面に垂直な方向のみ議論する。各金属内の電場の大きさを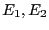 とする
と、電流は一定だから、
とする
と、電流は一定だから、
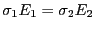 である。電場は不連続
になっているので、ガウスの法則より電荷が存在するはずである。その面密度を
である。電場は不連続
になっているので、ガウスの法則より電荷が存在するはずである。その面密度を
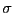 とすれば、
とすれば、
となる。従って、
となる。
Administrator
平成25年7月6日
![]() とする
と、電流は一定だから、
とする
と、電流は一定だから、
![]() である。電場は不連続
になっているので、ガウスの法則より電荷が存在するはずである。その面密度を
である。電場は不連続
になっているので、ガウスの法則より電荷が存在するはずである。その面密度を
![]() とすれば、
とすれば、