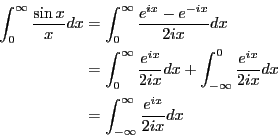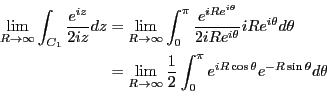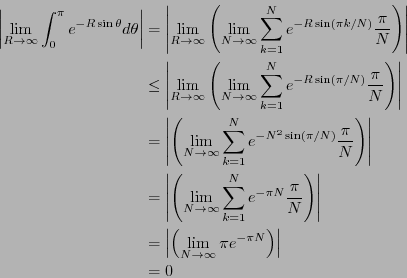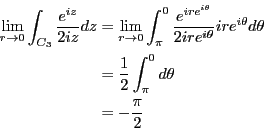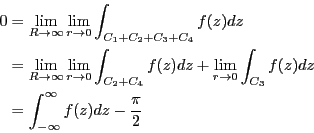===== 解答 =====
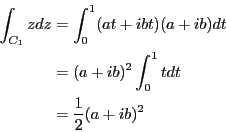
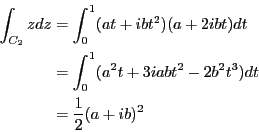
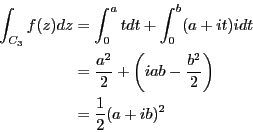
問題8.2
以下の積分経路について![]() を計算せよ。
を計算せよ。
===== 解答 =====
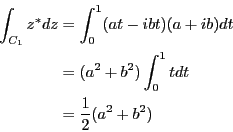
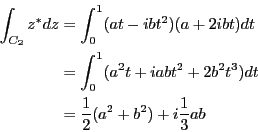
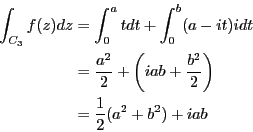
問題8.3
![]() を出発して
を出発して![]() を経由して
を経由して![]() と戻る直角三角形の経路を
と戻る直角三角形の経路を![]() として、
として、
===== 解答 =====
前問の解答より各辺の積分は求められている。従って、
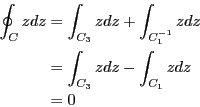
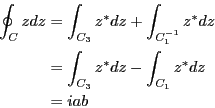
問題8.4
経路として半径1の円周をとり![]() から反時計回り(正の向き)に1周する場合
の
から反時計回り(正の向き)に1周する場合
の![]() の複素積分を求めよ。
の複素積分を求めよ。
===== 解答 =====
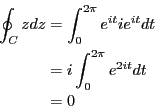
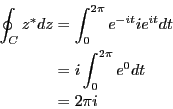
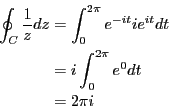
問題8.5
ヒント:
![]()
ヒント:グリーンの定理
===== 解答 =====
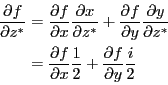
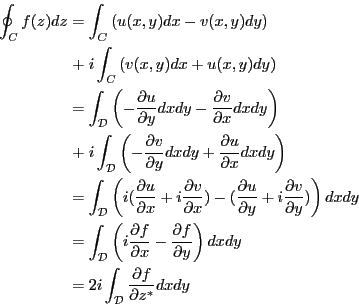
問題8.6
半径2で原点を中心とする円を経路![]() , 半径1で中心を
, 半径1で中心を![]() とする円
(
とする円
(![]() )を経路
)を経路![]() とする。
それぞれの経路に対して
とする。
それぞれの経路に対して
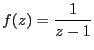
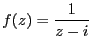
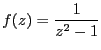
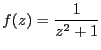
===== 解答 =====
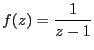 だから、
だから、
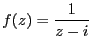 だから、
だから、
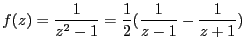 だから、
だから、
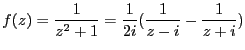 だから、
だから、
問題8.7
実変数関数
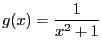 のフーリエ変換
のフーリエ変換
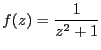 を考え、
を考え、
===== 解答 =====
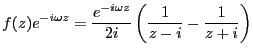 と変形できるので、その留数は
と変形できるので、その留数は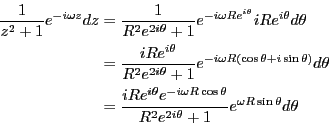
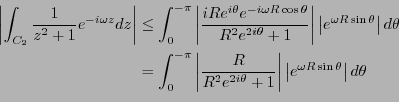
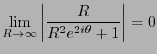 である。従って、極限値は0になることがわかる。
である。従って、極限値は0になることがわかる。
問題8.8
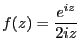 の複素積分を行え。
の複素積分を行え。
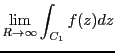 を計算せよ。
を計算せよ。
===== 解答 =====