



: 物質中の静電界の基本法則のまとめ
: 物質中の電界と磁場
: 誘電体を入れたキャパシター
目次
誘電分極を起こした絶縁体内から分極の方向に長さ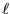 、断面積
、断面積
 の円柱を切り出したと考える。この時、この円柱の断面に
現れる電荷の密度が
の円柱を切り出したと考える。この時、この円柱の断面に
現れる電荷の密度が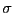 になったと仮定する。
正負の電荷の重心のズレを
になったと仮定する。
正負の電荷の重心のズレを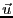 、また正の電荷の密度を
、また正の電荷の密度を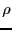 とす
ると、
とす
ると、
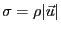 になる。ここで
大きさが
になる。ここで
大きさが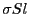 で向きが分極の方向を持ったベクトルを
考え、この円柱の「双極子モーメント」と呼ばう。
分極の強さを表すためには、単位体積あたりの
「双極子モーメント」を用い、これを「誘電分極」、「電気分極」
または「分極ベクトル」と呼ぶ。分極ベクトルは、
で向きが分極の方向を持ったベクトルを
考え、この円柱の「双極子モーメント」と呼ばう。
分極の強さを表すためには、単位体積あたりの
「双極子モーメント」を用い、これを「誘電分極」、「電気分極」
または「分極ベクトル」と呼ぶ。分極ベクトルは、
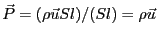 |
|
|
(3.29) |
である。電界が位置の関数だったり、物質が一様でなかったりする場合には、
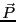 は位置
は位置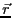 の関数のなることに注意。
の関数のなることに注意。
誘電体中の閉曲面 を考え、分極が生じた場合その曲面の内側から外側に動く電荷
を考察する。先ほどの
を考え、分極が生じた場合その曲面の内側から外側に動く電荷
を考察する。先ほどの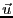 を用いると、
を用いると、
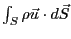 となる。
となる。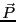 の定義により、この電荷は
の定義により、この電荷は
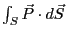 となる。この閉局面
となる。この閉局面 内の電荷は最初ゼロ
であったので、分極が起こった後に残る電荷
内の電荷は最初ゼロ
であったので、分極が起こった後に残る電荷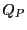 は
は
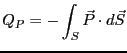 |
|
|
(3.30) |
となる。分極は正負の電荷の重心のズレ、
または電気双極子を持った分子の向きがそろう
ことによって生じるので、分極電荷はかならず正負が組になって
現れ、物質全体ではその和はゼロになる。それに対して分離できる通常の電荷を
真電荷と呼ぶ。
式3.35に対してガウスの定理を適用すると、分極電荷の密度
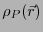 と分極ベクトル
と分極ベクトル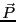 の間の関係が得られる。
の間の関係が得られる。
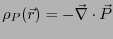 |
|
|
(3.31) |
物質中のガウスの法則では、分極電荷も考慮しないといけない。微分形で書くと、
となる。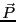 を使って変形すると、
を使って変形すると、
となる。物質中の電束密度ベクトルとして、
を定義すると、物質中のガウスの法則は、
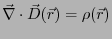 |
|
|
(3.32) |
となり、真空中と同じ形になる。
通常、分極は電界に比例する。また、多くの物質(等方性物質)では
電場に比例するだけでなく、方向も一致する。すなわち、
となる。ここで、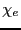 をその誘電体の電気感受率と言う。
をその誘電体の電気感受率と言う。
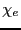 を使うと、
を使うと、
となり、電束密度は電界に比例することになる。そこで、
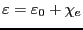 |
|
|
(3.33) |
を定義して、その物質の誘電率という。当然、
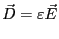 |
|
|
(3.34) |
となる。また、真空の誘電率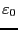 と
と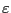 の比を比誘電率と
呼ぶ。
の比を比誘電率と
呼ぶ。




: 物質中の静電界の基本法則のまとめ
: 物質中の電界と磁場
: 誘電体を入れたキャパシター
目次
Administrator
平成25年7月6日
![]() を考え、分極が生じた場合その曲面の内側から外側に動く電荷
を考察する。先ほどの
を考え、分極が生じた場合その曲面の内側から外側に動く電荷
を考察する。先ほどの![]() を用いると、
を用いると、
![]() となる。
となる。![]() の定義により、この電荷は
の定義により、この電荷は
![]() となる。この閉局面
となる。この閉局面![]() 内の電荷は最初ゼロ
であったので、分極が起こった後に残る電荷
内の電荷は最初ゼロ
であったので、分極が起こった後に残る電荷![]() は
は
![]() と分極ベクトル
と分極ベクトル![]() の間の関係が得られる。
の間の関係が得られる。