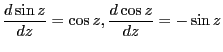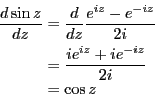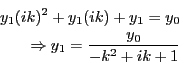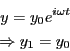: バンド構造
: 複素数の復習I
: ド・モアブルの公式
目次
問題2.1
複素数の基本的な性質を確認せよ。
===== 解答 =====
省略。
問題2.2
二つの複素数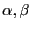 の大きさが両方とも1より小さい場合、
次の不等式
の大きさが両方とも1より小さい場合、
次の不等式
が成り立つことを示せ。
===== 解答 =====
問題2.3
-
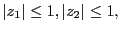 ならば、
ならば、
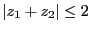 となることを
複素平面を使って説明せよ。
となることを
複素平面を使って説明せよ。
-
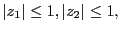 ならば、
ならば、
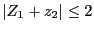 となることを
計算によって説明せよ。
となることを
計算によって説明せよ。
- 任意の
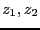 に対して
に対して
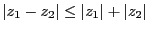 となることを
複素平面を使って説明せよ。
となることを
複素平面を使って説明せよ。
- 任意の
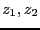 に対して
に対して
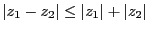 となることを
計算によって説明せよ。
となることを
計算によって説明せよ。
===== 解答 =====
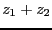 の複素平面上の位置は
の複素平面上の位置は
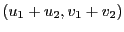 となる。この点は
原点から半径2の円より外にでることはない。
となる。この点は
原点から半径2の円より外にでることはない。
-
従って、証明できた。
- 原点、
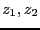 に対応する点を各頂点とする三角形を考える。説明す
べき式は「三角形の2辺の和は残りの辺よりも長い」という三角不等式を表してい
ることになる。
に対応する点を各頂点とする三角形を考える。説明す
べき式は「三角形の2辺の和は残りの辺よりも長い」という三角不等式を表してい
ることになる。
-
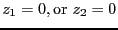 ならば、等号が成立する。
ここで、
ならば、等号が成立する。
ここで、
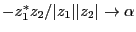 と置けば、
と置けば、
となる。ここで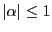 なので、(1,2)より証明が終わる。
なので、(1,2)より証明が終わる。
問題2.4
以下の複素数に対して極形式
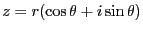 を求めよ。
を求めよ。
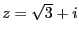
-
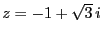
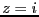
===== 解答 =====
-
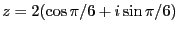
-
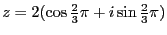
-
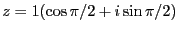
問題2.5
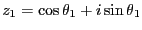 ,
,
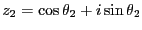 とする。
とする。
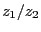 を計算せよ。
を計算せよ。
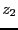 で割ることの複素平面上の意味を説明せよ。
で割ることの複素平面上の意味を説明せよ。
===== 解答 =====
-
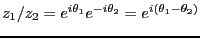
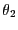 だけ逆回転すること。
だけ逆回転すること。
問題2.6
オイラーの公式を証明せよ。
===== 解答 =====
問題2.7
オイラーの公式を用いて、以下の計算を行なえ。
ヒント:
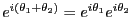
-
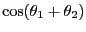
-
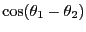
-
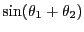
-
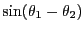
===== 解答 =====
問題2.8
ド・モアブルの公式を使って以下の方程式の解を求めよ。
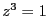
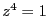
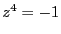
===== 解答 =====
-
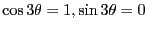 より、
より、
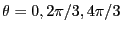 .
.
-
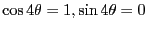 より、
より、
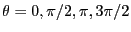 .
.
-
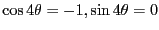 より、
より、
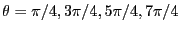 .
.
問題2.9
以下の計算を行なえ。
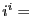
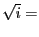
===== 解答 =====
-
-
問題2.10
複素数関数
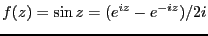 について
について
-
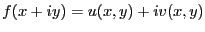 としたときの
としたときの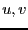 を求めよ。
を求めよ。
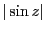 を計算せよ。
を計算せよ。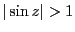 となる
となる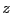 は存在するか?
は存在するか?
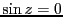 の方程式を解け。
の方程式を解け。
===== 解答 =====
-
-
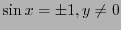 であれば、
であれば、
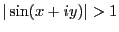 となる。
となる。
-
でなければならない。
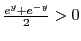 より
より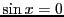 でなければなら
ない。一方、
でなければなら
ない。一方、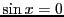 の場合、
の場合、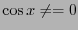 である。従って、
である。従って、
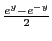 でなければならない。すなわち、
でなければならない。すなわち、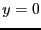 である。
である。
問題2.11
以下の関数の微分可能性について微分の定義に基づいて判定せよ。
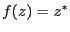
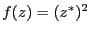
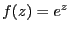
===== 解答 =====
-
最後のところで、
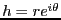 と置いた。
と置いた。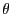 に依存するので、微分
可能ではない。
に依存するので、微分
可能ではない。
-
最後のところで、
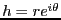 と置いた。
と置いた。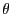 に依存するので、微分
可能ではない。
に依存するので、微分
可能ではない。
-
従って、微分可能である。
問題2.12
以下の関数の微分可能性についてコーシー・リーマンの関係式から判定せよ。
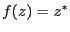
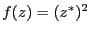
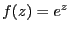
===== 解答 =====
-
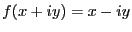 すなわち、
すなわち、
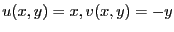 である。
である。
よって、正則ではなく微分可能ではない。
-
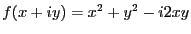 すなわち、
すなわち、
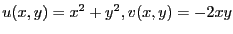 である。
である。
よって、正則ではなく微分可能ではない。
-
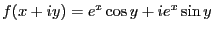 すなわち、
すなわち、
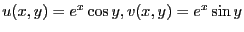 である。
である。
よって、正則であり微分可能である。
問題2.13
複素関数
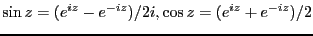 につ
いて
につ
いて
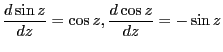 |
|
|
(2.7) |
であることを示せ。
===== 解答 =====
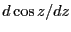 も同様に行う。
も同様に行う。
問題2.14
- 以下の微分方程式(
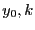 は定数)
は定数)
で
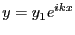 が解になるように、定数
が解になるように、定数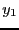 を定めよ。
を定めよ。
- 以下の微分方程式(
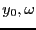 は定数)
は定数)
で
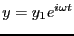 が解となるように定数
が解となるように定数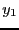 を定めよ。
を定めよ。
===== 解答 =====
-
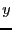 を
を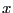 で偏微分してもゼロなので、
で偏微分してもゼロなので、




: バンド構造
: 複素数の復習I
: ド・モアブルの公式
目次
Administrator
平成25年1月3日
![]() の大きさが両方とも1より小さい場合、
次の不等式
の大きさが両方とも1より小さい場合、
次の不等式
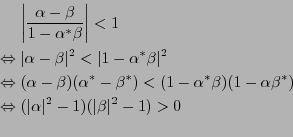
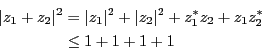
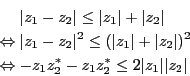
![]() を求めよ。
を求めよ。
![]() ,
,
![]() とする。
とする。
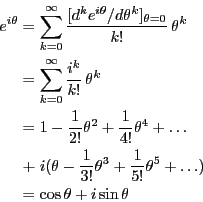
![]()
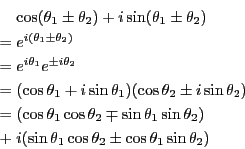
![]() について
について
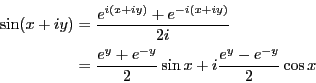
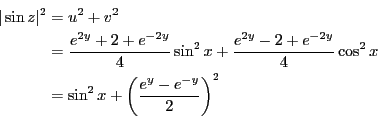
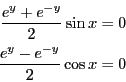
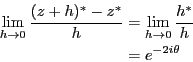
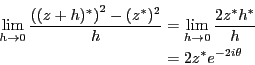
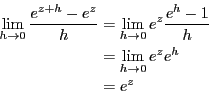
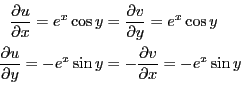
![]() につ
いて
につ
いて